题目内容
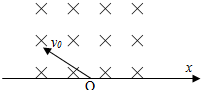 如图所示,在轴上方有一范围无限大的垂直纸面向里的匀强磁场B,一个质量为m、电荷量为-q的粒子以速度v0从坐标原点O射人磁场,v0与负x轴方向的夹角为θ,不计粒子重力,求:
如图所示,在轴上方有一范围无限大的垂直纸面向里的匀强磁场B,一个质量为m、电荷量为-q的粒子以速度v0从坐标原点O射人磁场,v0与负x轴方向的夹角为θ,不计粒子重力,求:(1)粒子在磁场中飞行的时间和飞出磁场的点的x坐标;
(2)粒子在磁场中运动时离x轴能达到的最大距离是多少?
(3)如果把上面所说的磁场改为方向垂直纸面向里的电场强度为E的匀强电场,则经过t秒钟,带电粒子的速度大小和方向如何?
分析:(1)粒子进入磁场后受到洛伦兹力作用而做匀速圆周运动,画出轨迹,由几何知识确定出轨迹对应的圆心角,即可求出时间
(2)由牛顿第二定律求出轨迹的半径,结合圆心角,即可求出粒子离开磁场时与原点O之间的距离.
(3)带电粒子进入电场后作类平抛运动,由牛顿第二定律和运动学公式可求解.
(2)由牛顿第二定律求出轨迹的半径,结合圆心角,即可求出粒子离开磁场时与原点O之间的距离.
(3)带电粒子进入电场后作类平抛运动,由牛顿第二定律和运动学公式可求解.
解答:解:(1)粒子在磁场中受洛伦兹力作用做匀速圆周运动,所以有:qBv0=
则有:R=
,
所以由几何关系得:x=2Rsinθ=
又T=

所以粒子在磁场中飞行时间t=
?
=
;
(2)如图,粒子在磁场中运动时离开x轴的最大距离为:
H=R+Rcosθ=R(1+cosθ)=
(1+cosθ)
(3)带电粒子进入电场后作类平抛运动,v0方向匀速运动,电场方向匀加速运动
由牛顿第二定律得加速度a=
,方向垂直纸面向外
t秒后,电场方向上速度v1=at=
t
所以合速度v=
=
方向x轴正方向夹角为α
则tanα=
=
=
,
即α=arctan
;
答:(1)粒子在磁场中飞行的时间为
,飞出磁场的点的x坐标为
(2)粒子在磁场中运动时离x轴能达到的最大距离是
(1+cosθ)
(3)如果把上面所说的磁场改为方向垂直纸面向里的电场强度为E的匀强电场,则经过t秒钟,带电粒子的速度为
,
方向与x轴正方向夹角为arctan
.
m
| ||
| R |
则有:R=
| mv0 |
| qB |
所以由几何关系得:x=2Rsinθ=
| 2mv0sinθ |
| qR |
又T=
| 2πm |
| qB |

所以粒子在磁场中飞行时间t=
| 2π-2θ |
| 2π |
| 2πm |
| qB |
| 2(π-θ)m |
| qB |
(2)如图,粒子在磁场中运动时离开x轴的最大距离为:
H=R+Rcosθ=R(1+cosθ)=
| mv0 |
| qB |
(3)带电粒子进入电场后作类平抛运动,v0方向匀速运动,电场方向匀加速运动
由牛顿第二定律得加速度a=
| qE |
| m |
t秒后,电场方向上速度v1=at=
| qE |
| m |
所以合速度v=
v02+
|
|
方向x轴正方向夹角为α
则tanα=
| v0 |
| v1 |
| v0 | ||
|
| mv0 |
| qEt |
即α=arctan
| mv0 |
| qEt |
答:(1)粒子在磁场中飞行的时间为
| 2(π-θ)m |
| qB |
| 2mv0sinθ |
| qR |
(2)粒子在磁场中运动时离x轴能达到的最大距离是
| mv0 |
| qB |
(3)如果把上面所说的磁场改为方向垂直纸面向里的电场强度为E的匀强电场,则经过t秒钟,带电粒子的速度为
|
方向与x轴正方向夹角为arctan
| mv0 |
| qEt |
点评:本题考查带电粒子在匀强磁场中的运动,根据t=
T,θ是轨迹的圆心角,根据几何知识,轨迹的圆心角等于速度的偏向角.
| θ |
| 2π |

练习册系列答案
相关题目
 轴上方有一匀强电场,场强大小为
轴上方有一匀强电场,场强大小为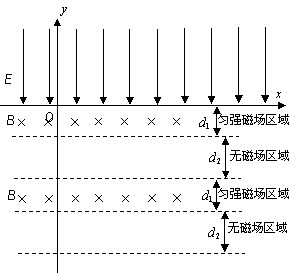
 轴上方有一匀强电场,场强大小为
轴上方有一匀强电场,场强大小为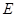 ,方向竖直向下。在
,方向竖直向下。在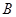 ,方向垂直于纸面向里。在
,方向垂直于纸面向里。在 ,离原点距离为
,离原点距离为 。现有一带电量为
。现有一带电量为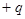 ,质量为
,质量为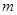 的粒子,不计重力,从
的粒子,不计重力,从 区间某点由静止开始释放后,能经过
区间某点由静止开始释放后,能经过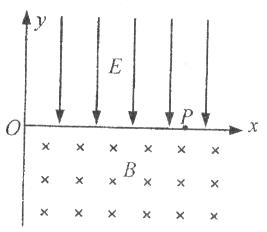
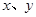 应满足的关系式?
应满足的关系式?