题目内容
设行星绕恒星运动轨道为圆形，则它运动的周期平方与轨道半径的三次方之比
=K为常数，此常数的大小（ ）
| T2 |
| R3 |
| A、只与恒星质量有关，恒星质量越大，K值越小 |
| B、与恒星质量和行星质量均有关，二者质量乘积越大，K值越大 |
| C、只与行星质量有关 |
| D、与恒星和行星的速度有关 |
分析：开普勒第三定律中的公式
=K，可知半长轴的三次方与公转周期的二次方成正比．
| T2 |
| R3 |
解答：解：令恒星质量为M，行星质量为m，轨道半径为r，根据万有引力提供圆周运动向心力有：
=
整理可得：
=
因为4π2为常量可知，比值
只与恒星质量M有关．故A正确，BCD错误．
故选：A．
| GMm |
| r2 |
| m4π2r |
| T2 |
整理可得：
| T2 |
| r3 |
| 4π2 |
| GM |
因为4π2为常量可知，比值
| T2 |
| r3 |
故选：A．
点评：行星绕太阳虽然是椭圆运动，但我们可以当作圆来处理，同时值得注意是周期是公转周期
练习册系列答案
相关题目
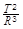= k 为常数，此常数的大小（ ）