题目内容
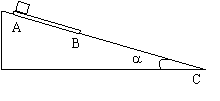
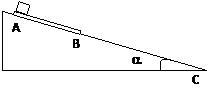 如图所示,倾角a = 37°的固定斜面上放一块质量M = 1 kg,长度 L = 3 m的薄平板AB。平板的上表面光滑,其下端B与斜面底端C的距离为7m。在平板的上端A处放一质量m = 0.6kg的滑块,开始时使平板和滑块都静止,之后将它们无初速释放。假设平板与斜面间、滑块与斜面间的动摩擦因数均为m = 0.5,求滑块、平板下端B到达斜面底端C的时间差是多少?(sin37
如图所示,倾角a = 37°的固定斜面上放一块质量M = 1 kg,长度 L = 3 m的薄平板AB。平板的上表面光滑,其下端B与斜面底端C的距离为7m。在平板的上端A处放一质量m = 0.6kg的滑块,开始时使平板和滑块都静止,之后将它们无初速释放。假设平板与斜面间、滑块与斜面间的动摩擦因数均为m = 0.5,求滑块、平板下端B到达斜面底端C的时间差是多少?(sin37![]() =0.6 cos37
=0.6 cos37![]() =0.8 g=10m/s
=0.8 g=10m/s![]() )
)
1.65s
解析:
对薄板由于Mgsin37![]() ﹤m(M+m)gcos37
﹤m(M+m)gcos37![]() 故滑块在薄板上滑动时,薄板静止不动.
故滑块在薄板上滑动时,薄板静止不动.
对滑块:在薄板上滑行时加速度a![]() =gsin37
=gsin37![]() =6m/s
=6m/s![]() ,至B点时速度V=
,至B点时速度V=![]() =6m/s。
=6m/s。
滑块由B至C时的加速度a![]() = gsin37
= gsin37![]() -mgcos37
-mgcos37![]() =2 m/s
=2 m/s![]() ,滑块由B至C用时t,由L
,滑块由B至C用时t,由L![]() =Vt+
=Vt+![]() a
a![]() t
t![]()
即t![]() +6t-7=0 解得t=1s
+6t-7=0 解得t=1s
对薄板:滑块滑离后才开始运动,加速度a= gsin37![]() -mgcos37
-mgcos37![]() =2 m/s
=2 m/s![]() ,滑至C端用时t
,滑至C端用时t![]() =
=![]() =
=![]() s
s
故滑块、平板下端B到达斜面底端C的时间差是△t= t![]() -t=
-t=![]() -1=1.65s
-1=1.65s

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 如图所示,倾角θ=30°的斜面上有一重为G的物体,在与斜面底边平行的水平推力作用下沿斜面上的虚线匀速运动,若图中φ=45°,则( )
如图所示,倾角θ=30°的斜面上有一重为G的物体,在与斜面底边平行的水平推力作用下沿斜面上的虚线匀速运动,若图中φ=45°,则( )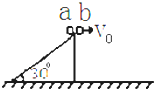 如图所示,小球a、b的质量分别是m和2m.a从倾角为30°的光滑固定斜面的顶端无初速度下滑,b从与斜面等高度处以初速度v0平抛.关于a、b落地前的运动过程,下列说法不正确的有( )
如图所示,小球a、b的质量分别是m和2m.a从倾角为30°的光滑固定斜面的顶端无初速度下滑,b从与斜面等高度处以初速度v0平抛.关于a、b落地前的运动过程,下列说法不正确的有( )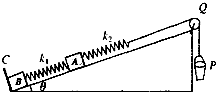 如图所示,倾角为θ的固定光滑斜面底部有一垂直斜面的固定挡板C,劲度系数为k1的轻弹簧两端分别与质量都为m的物体A和B连接,劲度系数为k2的轻弹簧一端与A连接,另一端通过一跨过光滑滑轮Q的轻绳与一轻质小桶P相连,B靠在挡板C处,A和B均静止,现缓慢地向小桶P内加入细砂,当B与挡板C间挤压力恰好为零时,小桶P内加入的细砂质量为
如图所示,倾角为θ的固定光滑斜面底部有一垂直斜面的固定挡板C,劲度系数为k1的轻弹簧两端分别与质量都为m的物体A和B连接,劲度系数为k2的轻弹簧一端与A连接,另一端通过一跨过光滑滑轮Q的轻绳与一轻质小桶P相连,B靠在挡板C处,A和B均静止,现缓慢地向小桶P内加入细砂,当B与挡板C间挤压力恰好为零时,小桶P内加入的细砂质量为