题目内容
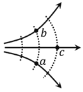
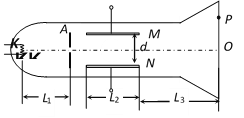
【题目】如图所示为一真空示波管,电子从灯丝K发出(初速度不计),经灯丝与A板间的加速电压U1加速,从A板中心孔沿中心线KO射出,K到A板中心的最短距离为L1,然后进入两块平行金属板M、N形成的偏转电场中(偏转电场可视为匀强电场),电子进入M、N间电场时的速度与电场方向垂直,电子经过电场后打在荧光屏上的P点。已知加速电压为U1,M、N两板间的电压为U2,两板间的距离为d,板长为L2,板右端到荧光屏的距离为L3,电子的质量为m,电荷量大小为e求:
(1)电子穿过A板时的速度大小v1;
(2)电子从偏转电场射出时的偏角的正切值tanθ;
(3)P点到O点的距离y。
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3)![]()
【解析】
(1)设电子经电压U1加速后的速度为v1,根据动能定理得:
![]()
解得:
![]()
(2)电子以速度v1进入偏转电场后,垂直于电场方向作匀速直线运动,沿电场方向作初速度为零的匀加速直线运动,设偏转电场的电场强度为E,电子在偏转电场运动的时间为t1,电子的加速度为a,离开偏转电场时相对于原运动方向的侧移量为y1,根据牛顿第二定律得
![]()
又
![]()
水平方向
![]()
竖直方向
![]()
电子离开偏转电场后做匀速直线运动,

(3)由几何关系有
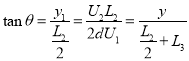
解得:
![]()

练习册系列答案
相关题目