题目内容
 如图所示,AB是一根粗细均匀的均质杆,用轻绳AO、BO挂于O点,OAB能绕O点在竖直平面转动.AO<BO,在A点挂一重物P,使AB保持水平,C为O点正下方的杆上一点,已知AC、BC部分的质量分别为m1、m2,重物P的质量为m3,则:m1+m3
如图所示,AB是一根粗细均匀的均质杆,用轻绳AO、BO挂于O点,OAB能绕O点在竖直平面转动.AO<BO,在A点挂一重物P,使AB保持水平,C为O点正下方的杆上一点,已知AC、BC部分的质量分别为m1、m2,重物P的质量为m3,则:m1+m3分析:以O点为支点,AC部分重心在AC中心,BC部分重心在BC的中点,根据力矩平衡条件列式分析;再对整体受力分析,运用共点力平衡条件列式分析.
解答:解:以O点为支点,AC部分重心在AC中心,BC部分重心在BC的中点,根据力矩平衡条件,有:
m3g?AC+m1g?
AC=m2g?
BC
由图象可以看出,AC≈
BC;
故m3+
m1=m2,故m1+m3>m3+
m1=m2
对杆和重物整体受力分析,受重力和两个拉力,如图:
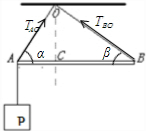
根据平衡条件,有:
TAOcosα=TBOcosβ
由于α>β,故TAO>TBO;
故答案为:>,>.
m3g?AC+m1g?
| 1 |
| 2 |
| 1 |
| 2 |
由图象可以看出,AC≈
| 1 |
| 2 |
故m3+
| 1 |
| 2 |
| 1 |
| 2 |
对杆和重物整体受力分析,受重力和两个拉力,如图:

根据平衡条件,有:
TAOcosα=TBOcosβ
由于α>β,故TAO>TBO;
故答案为:>,>.
点评:本题关键选定支点后,结合力矩平衡条件和共点力平衡条件列式分析,较难.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
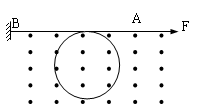
 (2013?安徽模拟)如图所示,AB是一根裸导线,单位长度的电阻为R0,一部分弯曲成直径为d的圆圈,圆圈导线相交处导电接触良好.圆圈所在区域有与圆圈平面垂直的均匀磁场,磁感强度为B0导线一端B点固定,A端在沿BA方向的恒力F作用下向右缓慢移动,从而使圆圈缓慢缩小.设在圆圈缩小过程中始终保持圆的形状,设导体回路是柔软的,此圆圈从初始的直径d到完全消失所需时间t为( )
(2013?安徽模拟)如图所示,AB是一根裸导线,单位长度的电阻为R0,一部分弯曲成直径为d的圆圈,圆圈导线相交处导电接触良好.圆圈所在区域有与圆圈平面垂直的均匀磁场,磁感强度为B0导线一端B点固定,A端在沿BA方向的恒力F作用下向右缓慢移动,从而使圆圈缓慢缩小.设在圆圈缩小过程中始终保持圆的形状,设导体回路是柔软的,此圆圈从初始的直径d到完全消失所需时间t为( ) (2013?普陀区一模)如图所示,AB是一根裸导线,单位长度的电阻为R0,一部分弯曲成半径为r0的圆圈,圆圈导线相交处导电接触良好.圆圈所在区域有与圆圈平面垂直的均匀磁场,磁感强度为B.导线一端B点固定,A端在沿BA方向的恒力F作用下向右缓慢移动,从而使圆圈缓慢缩小.设在圆圈缩小过程中始终保持圆的形状,导体回路是柔软的,在此过程中F所作功全部变为
(2013?普陀区一模)如图所示,AB是一根裸导线,单位长度的电阻为R0,一部分弯曲成半径为r0的圆圈,圆圈导线相交处导电接触良好.圆圈所在区域有与圆圈平面垂直的均匀磁场,磁感强度为B.导线一端B点固定,A端在沿BA方向的恒力F作用下向右缓慢移动,从而使圆圈缓慢缩小.设在圆圈缩小过程中始终保持圆的形状,导体回路是柔软的,在此过程中F所作功全部变为