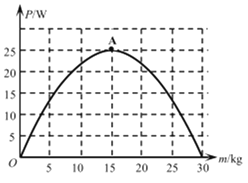
题目内容
【题目】如图所示，轻弹簧的两端与质量均为M的B、C两物块固定连接，静止在光滑水平面上，物块C紧靠挡板但不粘连．从一把玩具枪射出的子弹A，沿水平方向射入物块后留在物块内（作用时间极短），在此后的弹簧压缩和拉伸过程中弹簧都在弹性限度内．
（1）如果子弹质量为m，速度为v0，求弹簧第一次压缩最短时的弹性势能；
（2）如果玩具枪射出子弹时的动能恒为Ek，而子弹质量不同，之后的相互作用过程中，弹簧所能拉伸的最大长度不同，为使弹簧拉伸的长度最大，子弹的质量应是多少？此时的弹簧的弹性势能多大？
【答案】（1）
（2）
【解析】
（1）子弹射入木块B的过程，取向左为正方向，由动量守恒定律得
根据能量守恒定律得：弹簧第一次压缩最短时的弹性势能为：
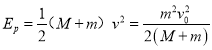
（2）设子弹的质量为m，玩具枪射出子弹时的速度为v0．当C离开挡板后，B、C速度相同时，弹簧伸长最长，此时弹性势能最大，设为Epm，B、C的共同速度为v′，C刚离开挡板时B的速度大小为v，方向向右
取向右为正方向，由动量守恒定律得
由机械能守恒定律得
．
结合
．
联立得到
，
求导得
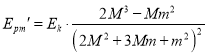
当 Epm′=0时，Epm最大，此时
此时的弹簧的弹性势能为
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
