题目内容
 (2013?广州三模)一绝缘“?”形杆由两段相互平行的足够长的水平直杆PQ、MN和一半径为R的光滑半圆环MAP组成,固定在竖直平面内,其中MN杆是光滑的,PQ杆是粗糙的,整个装置处在水平向左的匀强电场中.在PM左侧区域足够大的范围内同时存在垂直竖直平面向里的匀强磁场,磁感应强度为B.现将一质量为m、带正电电量为q的小环套在MN杆上,小环所受的电场力为重力的
(2013?广州三模)一绝缘“?”形杆由两段相互平行的足够长的水平直杆PQ、MN和一半径为R的光滑半圆环MAP组成,固定在竖直平面内,其中MN杆是光滑的,PQ杆是粗糙的,整个装置处在水平向左的匀强电场中.在PM左侧区域足够大的范围内同时存在垂直竖直平面向里的匀强磁场,磁感应强度为B.现将一质量为m、带正电电量为q的小环套在MN杆上,小环所受的电场力为重力的| 1 | 2 |
(1)若将小环由D点静止释放,则刚好能到达P点,求DM间的距离
(2)在满足第一问的情况下,小环在A点对圆环的压力
(3)若将小环由M点右侧5R处静止释放,设小环与PQ杆间的动摩擦因数为μ,小环所受最大静摩擦力与滑动摩擦力大小相等,求小环在整个运动过程中克服摩擦力所做的功.
分析:(1)小环从D至P过程中,根据动能定理结合电场力与重力关系,即可求解;
(2)小环从D至A的过程,根据动能定理;对小环在A点受力分析由牛顿第二定律及牛顿第三定律即可求解;
(3)根据速度为零分电场力小于等于最大静摩擦力与大于最大静摩擦力,由动能定理分别求出过程中克服摩擦力所做的功.
(2)小环从D至A的过程,根据动能定理;对小环在A点受力分析由牛顿第二定律及牛顿第三定律即可求解;
(3)根据速度为零分电场力小于等于最大静摩擦力与大于最大静摩擦力,由动能定理分别求出过程中克服摩擦力所做的功.
解答:解:(1)设电场强度为E,DM距离为L,对小环从D至P,由动能定理:
EqL-mg?2R=0-0 ①
题意有Eq=
mg ②
结合得 L=4R ③
(2)设小环在A点速度为vA,对小环从D至A的过程,由动能定理:
Eq?5R-mgR=
m
-0 ④
由小环在A点的受力分析及牛顿第二定律得:N-Eq-BqvA=
⑤
由④⑤式可得N=
mg+Bq
,⑥
根据牛顿第三定律,小环在A点对圆环的压力大小为N=
mg+Bq
,方向水平向左.
(3)小环首次到P点速度不为零,将向右运动,当速度为零时,若满足
(i)Eq≤fm=μmg,即μ≥
,小环将保持静止.设此时小环距P点水平距离为x,
则对全程由动能定理:
Eq(5R-x)-mg?2R-μmgx=0-0 ⑦
则克服摩擦力做功Wf=μmgx=
⑧
(ii) Eq>fm=μmg,即μ<
,小环将来回往复运动,最终会在P点的速度减为零.
则对全程由动能定理:Eq?5R-mg?2R-Wf=0-0 ⑨
得克服摩擦力做功Wf=
mgR
答:(1)若将小环由D点静止释放,则刚好能到达P点,求DM间的距离为4R;
(2)在满足第一问的情况下,小环在A点对圆环的压力大小为
mg+Bq
,方向水平向左;
(3)若将小环由M点右侧5R处静止释放,当电场力小于等于最大静摩擦力时,小环在整个运动过程中克服摩擦力所做的功为
;当电场力大于最大静摩擦力时,小环在整个运动过程中克服摩擦力所做的功为
mgR.
EqL-mg?2R=0-0 ①
题意有Eq=
| 1 |
| 2 |
结合得 L=4R ③
(2)设小环在A点速度为vA,对小环从D至A的过程,由动能定理:
Eq?5R-mgR=
| 1 |
| 2 |
| v | 2 A |
由小环在A点的受力分析及牛顿第二定律得:N-Eq-BqvA=
m
| ||
| R |
由④⑤式可得N=
| 7 |
| 2 |
| 3gR |
根据牛顿第三定律,小环在A点对圆环的压力大小为N=
| 7 |
| 2 |
| 3gR |
(3)小环首次到P点速度不为零,将向右运动,当速度为零时,若满足
(i)Eq≤fm=μmg,即μ≥
| 1 |
| 2 |
则对全程由动能定理:
Eq(5R-x)-mg?2R-μmgx=0-0 ⑦
则克服摩擦力做功Wf=μmgx=
| μmgR |
| 1+2μ |
(ii) Eq>fm=μmg,即μ<
| 1 |
| 2 |
则对全程由动能定理:Eq?5R-mg?2R-Wf=0-0 ⑨
得克服摩擦力做功Wf=
| 1 |
| 2 |
答:(1)若将小环由D点静止释放,则刚好能到达P点,求DM间的距离为4R;
(2)在满足第一问的情况下,小环在A点对圆环的压力大小为
| 7 |
| 2 |
| 3gR |
(3)若将小环由M点右侧5R处静止释放,当电场力小于等于最大静摩擦力时,小环在整个运动过程中克服摩擦力所做的功为
| μmgR |
| 1+2μ |
| 1 |
| 2 |
点评:本题考查动能定理、牛顿第二定律、牛顿第三定律,及向心力表达式.强调动能定理选取过程的重要性与做功的正负值.最后还注意克服摩擦力做功的分类性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013?广州三模)如图,相距L的光滑金属导轨,半径为R的
(2013?广州三模)如图,相距L的光滑金属导轨,半径为R的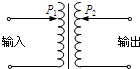 (2013?广州三模)在家用交流稳压器中,变压器的原、副线圈都带有滑动头P1、P2,如图所示.当变压器输入电压发生变化时,可以上下调节P1、P2的位置,使输出电压稳定在220V上.现发现输出电压低于220V,下列措施正确的是( )
(2013?广州三模)在家用交流稳压器中,变压器的原、副线圈都带有滑动头P1、P2,如图所示.当变压器输入电压发生变化时,可以上下调节P1、P2的位置,使输出电压稳定在220V上.现发现输出电压低于220V,下列措施正确的是( )
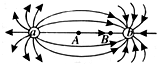 (2013?广州三模)如图所示为点电荷a、b所形成的电场线分布,以下说法正确的是( )
(2013?广州三模)如图所示为点电荷a、b所形成的电场线分布,以下说法正确的是( )