Question

【题目】如图所示，真空中有一匀强电场（图中未画出），电场方向与圆周在同一平面内，△ABC是圆的内接直角三角形，∠ACB=26.5°，O为圆心，半径R=5cm。位于A处的粒子源向平面内各个方向发射初动能均为8eV、电荷量+e的粒子，有些粒子会经过圆周上不同的点，其中到达B点的粒子动能为12eV，达到C点的粒子电势能为-4eV（取O点电势为零）。忽略粒子的重力和粒子间的相互作用，sin53°=0.8。下列说法正确的是

A.匀强电场的场强大小为100V/m

B.圆周上B、C两点的电势差为-4V

C.圆周上A、C两点的电势差为12V

D.当某个粒子经过圆周上某一位置时，可以具有6eV的电势能，且同时具有6eV的动能

Answer 1

【答案】A

【解析】

根据电势的定义可以求出C点的电势

根据匀强电场的特征可知：

UAO=UOC=4V

解得：

。

根据动能定理

，

解得：

。

由于B点的电势等于O点的电势等于0，所以O与B是等势点，连接OB，则OB为匀强电场的等势面，过A点做OB的垂线交OB与D点，则AD的方向就是该电场的场强方向，如图：

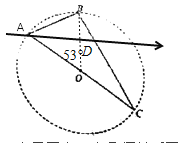
根据几何关系可知

∠AOB=53°，AD＝0.04m。

由于OBD是等势面，所以

。

故A正确；

B. 圆周上B、C两点的电势差为

故B错误；

C. 圆周上A、C两点的电势差为

故C错误；

D. 该圆周上电势最高的点到比O点高：

，

所以最大电势能只能是5eV。故D错误。