题目内容
如图所示，一人通过大小不计的光滑定滑轮用细线拉一质量为m的物体，开始时手拉的绳头在滑轮正下方H处，当保持这一高度向右走，人的速度恒为v．试求在从A点走到B点的过程中：（1）物体上升的高度；
（2）人对物体所做的功．
解：（1）由图中几何关系可得：物体上升的高度为
h=H/Sin30°-H/Sin60°
（2）由动能定理和题意条件可得：
W人-mgh=
mVB2-
mVA2VB=VA=V
上述解法正确吗？若你认为是正确的话，则解出其结果，若你认为不正确的话，则列式解出你认为正确的结果．
【答案】分析：该题中需要对人的速度进行分解．分解成沿着绳子的方向与垂直与绳子的方向的两个分速度，然后再使用动能定律解题．
解答：解：（1）解法正确
（2）解法不正确
在A和B 两个位置时物体的速度：vB=vcos30° vA=vcos60°
由动能定理得：W人-mgh=
mVB2-
mVA2
即：W人-mgh=
m（Vcos30°）2-
m（Vcos60°）2
代入数据，解得：W人=
mv2+
（3-
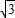）mgH
答：物体上升的高度：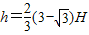
，人对物体做的功：W人=
mv2+
（3-
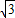）mgH
点评：该题只把人的速度分解成沿着绳子的方向与垂直与绳子的方向的两个分速度是解决问题的关键．属于中档题目．
解答：解：（1）解法正确
（2）解法不正确
在A和B 两个位置时物体的速度：vB=vcos30° vA=vcos60°
由动能定理得：W人-mgh=
mVB2-mVA2即：W人-mgh=
m（Vcos30°）2- m（Vcos60°）2代入数据，解得：W人=
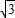mv2+（3-）mgH 答：物体上升的高度：
，人对物体做的功：W人=mv2+（3-）mgH点评：该题只把人的速度分解成沿着绳子的方向与垂直与绳子的方向的两个分速度是解决问题的关键．属于中档题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
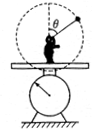如图所示，一质量为M的人站在台秤上，手拿一个质量为m、悬线长为R的小球（其中M＞m），在竖直平面内使小球做圆周运动，且小球恰好能通过圆轨道的最高点．求：
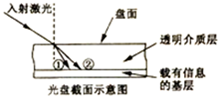（2012?莆田模拟）光盘上的信息通常是通过激光束来读取的．若激光束不是垂直人射到盘面上，则光线在进入透明介质层时会发生偏折而改变行进方向．如图所示为一束激光（红光、蓝光混合）入射到光盘盘面上后的折射情况，据此下列判断中正确的是（ ）
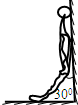如图所示，一人重为G，伸直腿斜靠在竖直墙上，腿与墙壁的夹角为30°，设腿的方向上的延长线恰通过人的重心，墙是光滑的，则双腿对人的支持力为多大？