题目内容
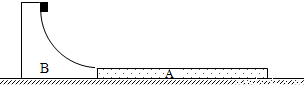
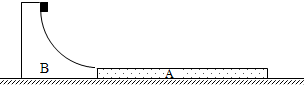
如图所示,固定于光滑地面上的四分之一圆弧轨道B,表面光滑,半径R=0.8m.地面上紧靠轨道B放置着足够长的木板A,木板A的上表面与轨道B末端相切,小物块由圆弧轨道顶端无初速滑下.已知木板A质量为M=6kg,小物块质量为m=2kg,小物块与木板之间动摩擦因数μ=0.5,取g=10m/s2.求:
(1)小物块刚滑上木板A时速度的大小?
(2)小物块与木板A摩擦所产生的热量是多少?
(3)小物块在木板上滑行的距离是多少?
(1)小物块刚滑上木板A时速度的大小?
(2)小物块与木板A摩擦所产生的热量是多少?
(3)小物块在木板上滑行的距离是多少?

分析:(1)小滑块滑到底部前,只有重力做功,机械能守恒,重力势能的减小量等于动能的增加量,根据守恒定律列式求解;
(2)滑块与木板A系统动量守恒,根据动量守恒定律求解共同速度;系统机械能的减小量等于内能的增加量;
(3)根据Q=f?△S求解相对路程△S.
(2)滑块与木板A系统动量守恒,根据动量守恒定律求解共同速度;系统机械能的减小量等于内能的增加量;
(3)根据Q=f?△S求解相对路程△S.
解答:解:(1)设小物体刚滑上木板时速度为v1,由机械能守恒定律:mgR=
m
得:v1=
=
m/s=4m/s
(2)小物块与木板最终共速,系统动量守恒:mv1=(m+M)v2
得:v2=
=
m/s=1m/s
由能量守恒定律得:Q=
m
-
(m+M)
得:Q=12J
(3)设小物块在木板上滑行的距离为L,由功能关系:μmgL=Q
得:L=
=
m=1.2m
答:(1)小物块刚滑上木板A时速度的大小为4m/s;
(2)小物块与木板A摩擦所产生的热量是12J;
(3)小物块在木板上滑行的距离是1.2m.
| 1 |
| 2 |
| v | 2 1 |
得:v1=
| 2gh |
| 2×10×0.8 |
(2)小物块与木板最终共速,系统动量守恒:mv1=(m+M)v2
得:v2=
| mv1 |
| m+M |
| 2×4 |
| 2+6 |
由能量守恒定律得:Q=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
得:Q=12J
(3)设小物块在木板上滑行的距离为L,由功能关系:μmgL=Q
得:L=
| Q |
| μmg |
| 12 |
| 0.5×2×10 |
答:(1)小物块刚滑上木板A时速度的大小为4m/s;
(2)小物块与木板A摩擦所产生的热量是12J;
(3)小物块在木板上滑行的距离是1.2m.
点评:本题关键明确滑块和木板的运动规律,会运用动量守恒定律列式求解共同速度,知道内能的增加量等于一对滑动摩擦力做的功的绝对值.

练习册系列答案
相关题目
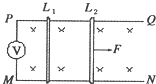 如图所示,固定于水平桌面上足够长的两平行光滑导轨PQ、MN,其电阻不计,间距d=0.5m,P、M两端接有一只理想电压表,整个装置处于竖直向下的磁感应强度B0=0.2T的匀强磁场中,两金属棒L1、L2平行地搁在导轨上,其电阻均为r=0.1Ω,质量分别为M1=0.3kg和M2=0.5kg.固定棒L1,使L2在水平恒力F=0.8N的作用下,由静止开始运动.试求:
如图所示,固定于水平桌面上足够长的两平行光滑导轨PQ、MN,其电阻不计,间距d=0.5m,P、M两端接有一只理想电压表,整个装置处于竖直向下的磁感应强度B0=0.2T的匀强磁场中,两金属棒L1、L2平行地搁在导轨上,其电阻均为r=0.1Ω,质量分别为M1=0.3kg和M2=0.5kg.固定棒L1,使L2在水平恒力F=0.8N的作用下,由静止开始运动.试求: (2010?普陀区一模)如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布.),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.求:
(2010?普陀区一模)如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布.),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.求: