题目内容
如图所示的装置可以测量飞行器在竖直方向上做匀加速直线运动的加速度．该装置是在矩形箱子的上、下壁上各安装一个可以测力的传感器，分别连接两根（可拉伸可压缩）的轻弹簧的一端，弹簧的另一端都固定在一个滑块上，滑块（可视为质点）套在光滑竖直杆上．现将该装置固定在一飞行器上，传感器P在上，传感器Q在下，P与Q之间距离恰好等于两弹簧原长之和．飞行器在地面静止时，传感器P、Q显示的弹力大小分别为12N和8N．求当飞行器竖直向上加速飞到离地面| R | 4 |
分析：首先弹簧一伸一缩，且总长等于两个原长之和，故其形变量应该相等，其由受力可知传感器受P的拉力，Q的支持力，重力，三力平衡，由此可以解得传感器的质量，PQ的进度系数的比值，再由万有引力等于重力．可以求得飞行器距离地面
处的重力加速度．再由牛顿第二定律可以求得此时飞行器的加速度．
| R |
| 4 |
解答：解：
由于两弹簧只能一伸一缩，故两弹簧对物体的弹力方向相同且形变量相等，故：FP+FQ-G=O
且：FP=k1x，FQ=k2x
解得：
m=2kg
k1=1.5k2
由：
mg′=G
mg=G
解得：
g′=
g=6.4m/s2
由胡克定律知：△F=k△x，P的弹力为18N，则Q的弹力为12N，有两弹簧的合力变为
FP′+FQ′=18+12=30N
由牛顿第二定律，得：
FP′+FQ′-mg′=ma
解得：
a=8.6m/s2
答：
此时飞行器的加速度是8.6m/s2
由于两弹簧只能一伸一缩，故两弹簧对物体的弹力方向相同且形变量相等，故：FP+FQ-G=O
且：FP=k1x，FQ=k2x
解得：
m=2kg
k1=1.5k2
由：
mg′=G
| Mm | ||
(R+
|
mg=G
| Mm |
| R2 |
解得：
g′=
| R2 | ||
(R+
|
由胡克定律知：△F=k△x，P的弹力为18N，则Q的弹力为12N，有两弹簧的合力变为
FP′+FQ′=18+12=30N
由牛顿第二定律，得：
FP′+FQ′-mg′=ma
解得：
a=8.6m/s2
答：
此时飞行器的加速度是8.6m/s2
点评：本题重点是解决弹力问题，首先必须依据题目判定弹簧的形变量是相等的，然后还的要求出进度系数的比值，由此才能知道P为18N时，Q的弹力．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
用如图所示的装置可以测量物体与桌面间的动摩擦因数．物体A放在带滑轮的水平长板上，用跨过滑轮（滑轮的大小可不计）的细线将A与另一个物体B相连．开始时B离地面高度为h，A离长板右端距离也为h，从静止释放B后，B会带动A做加速运动，当B落地时A正好离开长木板，最后A也落地（A在空中运动时细线始终处于松弛状态，A、B落地后均不会反弹）．已测得A、B的质量相等，h为已知，手边只有刻度尺一个测量工具．
（2008?宁波模拟）如图所示的装置可以测量飞行器在竖直方向上做匀加速直线运动的加速度，该装置是在矩形箱子的上、下壁上各安装一个可以测力的传感器，分别连接两根劲度系数相同（可拉伸可压缩）的轻弹簧的一端，弹簧的另一端都固定在一个滑块上，滑块套在光滑竖直杆上，现将该装置固定在一飞行器上，传感器P在上，传感器Q在下．飞行器在地面静止时，传感器P、Q显示的弹力大小均为10N．求：
如图所示的装置可以测量飞行器在竖直方向上做匀加速直线运动的加速度．该装置是在矩形箱子的上、下壁上各安装一个可以测力的传感器，分别连接两根劲度系数相同（可拉伸可压缩）的轻弹簧的一端，弹簧的另一端都固定在一个滑块上，滑块套在光滑竖直杆上．现将该装置固定在一飞行器上，传感器P在上，传感器Q在下．飞行器在地面静止时，传感器P、Q显示的弹力大小均为10N．求：
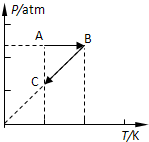
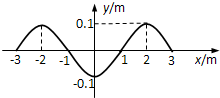
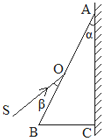
（3）快中子增殖反应堆中，使用的核燃料是钚239，裂变时释放出快中子，周围的铀238吸收快中子后变成铀239，铀239（92239U）很不稳定，经过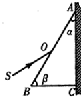
用如图所示的装置可以测定棱镜的折射率，其中ABC表示待测直角棱镜的横截面，棱镜的两个锐角α和β都是已知的，紧贴直角边AC的是一块平面镜，将束光线SO入射到棱镜的AB面上，适当调整SO的入射方向，使从AB面出射的光线与入射光线SO恰好重合，在这种情况下，仅需要测出一个物理量