题目内容
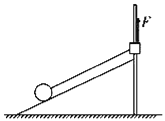
【题目】如图所示,半径为R的光滑圆环竖直固定,质量为3m的小球A套在圆环上;长为2R的刚性(既不伸长也不缩短)轻杆一端通过铰链与A连接,另一端通过铰链与滑块B连接;滑块B质量为m,套在水平固定的光滑杆上。水平杆与圆环的圆心O位于同一水平线上。现将A置于圆环的最高处并给A一微小扰动(初速度视为0),使A沿圆环顺时针自由下滑,不计一切摩擦,A、B均视为质点,重力加速度大小为g。求:
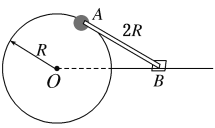
(1) A滑到与圆心O同高度时的速度大小;
(2) A下滑至杆与圆环第一次相切的过程中,杆对B做的功。
【答案】(1) ![]() (2)
(2) ![]()
【解析】
当A滑到与O同高度时,A的速度沿圆环切向向下,B的速度为零,对系统运用机械能守恒,求出A滑到与圆心O同高度时的速度大小;A下滑至杆与圆环第一次相切时,A的速度沿杆的方向,抓住A、B沿杆方向的分速度相等,结合系统机械能守恒求出B的速度,根据动能定理求出杆对B做的功。
(1)当A滑到与O同高度时,A的速度沿圆环切向竖直向下,B的速度为0,由机械能守恒定律得:3mgR=![]() ×3mv2,
×3mv2,
解得:![]()
(2)杆与圆环第一次相切时,A的速度沿杆方向,设为vA,此时B的速度设为vB,

根据杆不可伸长和缩短,得vA=vBcos θ。
由几何关系得![]()
球A下落的高度h=R(1-cos θ)=![]()
由机械能守恒定律得![]()
由动能定理得:![]()
解得:![]()

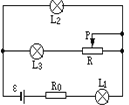
【题目】(1)在“探索弹力和弹簧伸长的关系”实验中,以下说法正确的是 .
A.弹簧被拉伸时,不能超出它的弹性限度 |
B.用悬挂砝码的方法给弹簧施加拉力,应保证弹簧位于竖直位置且处于平衡状态 |
C.用直尺测得弹簧的长度即为弹簧的伸长量 |
D.用几个不同的弹簧,分别测出几组拉力与伸长量,得出拉力与伸长量之比相等 |
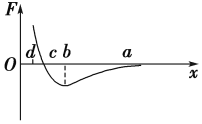
(2)某同学做“探索弹力和弹簧伸长的关系”的实验,他先把弹簧平放在桌面上使其自然伸长,用直尺测出弹簧的原长L0,再把弹簧竖直悬挂起来,挂上砝码后测出簧伸长后的长度L,把L﹣L0作为弹簧的伸长量x,这样操作,由于弹簧自身重力的影响,最后画出的图线可能是图中所示图象的 .