题目内容
(14分）如图，MN、PQ两条平行的光滑金属轨道与水平面成q=300角固定，轨距为L=1m，质量为m的金属杆A.b水平放置在轨道上，其阻值忽略不计。空间存在匀强磁场，磁场方向垂直于轨道平面向上，磁感应强度为B=0.5T。P、M间接有阻值R1的定值电阻，Q、N间接变阻箱R。现从静止释放A.b，改变变阻箱的阻值R，测得最大速度为vm，得到
与
的关系如图所示。若轨道足够长且电阻不计，重力加速度g取l0m/s2。求：
（1）金属杆的质量m和定值电阻的阻值R1；
（2）当变阻箱R取4Ω时，且金属杆A.b运动的加速度为
gsinq时，此时金属杆A.b运动的速度；
（3）当变阻箱R取4Ω时，且金属杆A.b运动的速度为
时，定值电阻R1消耗的电功率。
【答案】
（1）m=0.1kg，R=1Ω（2）v′＝0.8m/s（3）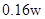
【解析】
试题分析：（1）（5 分）总电阻为R总＝R1R /(R1＋R)；I＝BLv/R总
当达到最大速度时金属棒受力平衡。mgsinq＝BIL=
，
，根据图像代入数据，可以得到棒的质量m=0.1kg，R=1Ω
（2）（5分）金属杆A.b运动的加速度为
gsinq时，I′＝BLv′/R总
根据牛顿第二定律F合＝mA.，mgsinq－BI’L＝mA.，
mgsinq－
＝ mgsinq，代入数据，得到v′＝0.8m/s
（3）（4分）当变阻箱R取4Ω时，根据图像得到vm=1.6m/s，
考点：考查了导体切割磁感线运动，
点评：此类型题目要重点做好受力分析及运动情景分析，用好共点力的平衡关系及牛顿第二定律等基本规律．
练习册系列答案
小学教材完全解读系列答案
相关题目
如图所示的竖直平面内有范围足够大、水平向左的匀强电场，电场强度为E．一绝缘弯杆由两段直杆和一半径R=1.6m的四分之一圆弧杆MN组成，固定在竖直面内，两直杆与圆弧杆的连接点分别是M、N，竖直杆PM和水平杆NQ均足够长，PMN段光滑．现有一质量为m1=0.2kg、带电荷量为+q的小环套在PM杆上，从M点的上方的D点静止释放，恰好能达到N点．已知q=2×10-2C，E=2×102N/m．g取10m/s2．
与
的关系如图所示。若轨道足够长且电阻不计，重力加速度g取l0m/s2。求：
gsinq时，此时金属杆A.b运动的速度；
时，定值电阻R1消耗的电功率。