题目内容
如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环.棒和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmg (k>1).断开轻绳,棒和环自由下落.假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失.棒在整个运动过程中始终保持竖直,空气阻力不计.求:(1)棒第一次与地面碰撞弹起上升过程中,环的加速度.
(2)从断开轻绳到棒与地面第二次碰撞的瞬间,棒运动的路程s.
(3)从断开轻绳到棒和环都静止,摩擦力对环及棒做的总功W.

(20分)(1)(5分) 设棒第一次上升过程中,环的加速度为a环 环所受合力F环=kmg-mg ① 由牛顿第二定律知 F环=ma环 ② 由①②式得a环=(k-1)g,方向竖直向上. (未说明a的方向扣1分)(2) (8分)设以地面为零势能面,向上为正方向,棒第一次落地的运度大小为v1, 由机械能守恒得  解得
解得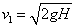 设棒弹起后的加速度为a棒 由牛顿第二定律a棒= - (k+1)g 棒第一次弹起的最大高度
设棒弹起后的加速度为a棒 由牛顿第二定律a棒= - (k+1)g 棒第一次弹起的最大高度 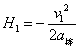 解得
解得  棒运动的路程s=H+2H1=
棒运动的路程s=H+2H1=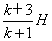 (3) (7分)设环相对棒的滑动距离为l根据能量守恒mgH+ mg(H+l) = kmgl摩擦力对棒及环做的总功 W= -kmgl
(3) (7分)设环相对棒的滑动距离为l根据能量守恒mgH+ mg(H+l) = kmgl摩擦力对棒及环做的总功 W= -kmgl 解得W=
解得W= 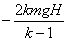 . (未表示W为负功扣2分)(3) 解法二棒第一次弹起经过t1时间,与环达到相同速度vl′环的速度 vl′= - vl +a环tl棒的速度 vl′= vl +a棒tl环的位移h环l=-vltl+
. (未表示W为负功扣2分)(3) 解法二棒第一次弹起经过t1时间,与环达到相同速度vl′环的速度 vl′= - vl +a环tl棒的速度 vl′= vl +a棒tl环的位移h环l=-vltl+ ;棒的位移h棒l=vltl+
;棒的位移h棒l=vltl+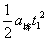 ; x1= h环l - h棒l解得x1=
; x1= h环l - h棒l解得x1= 棒环一起下落至地
棒环一起下落至地 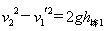 解得v2=
解得v2= 同理,环第二次相对棒的位移x2= h环2 - h棒2=
同理,环第二次相对棒的位移x2= h环2 - h棒2= ………… xn=
………… xn= 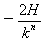 环相对棒的总位移x= x1 + x2 + … + xn + … W= -kmgx得W=
环相对棒的总位移x= x1 + x2 + … + xn + … W= -kmgx得W= 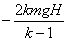 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环.棒和环的质量均为m,相互间最大静摩擦力认为等于滑动摩擦力,大小为1.5mg.断开轻绳,棒和环开始竖直下落.假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失.棒在整个运动过程中始终保持竖直,空气阻力不计.则( )
如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环.棒和环的质量均为m,相互间最大静摩擦力认为等于滑动摩擦力,大小为1.5mg.断开轻绳,棒和环开始竖直下落.假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失.棒在整个运动过程中始终保持竖直,空气阻力不计.则( )| A、棒第一次下落过程中,环做自由落体运动 | B、棒第一次与地面碰撞弹起上升过程中,棒做匀加速运动 | C、从断开轻绳到棒和环都静止的过程中,系统损失的机械能为2mgH | D、从断开轻绳到棒和环都静止,环相对于地面通过的位移为5H |
 (2007?江苏)如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环.棒和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmg(k>1).断开轻绳,棒和环自由下落.假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失.棒在整个运动过程中始终保持竖直,空气阻力不计.求:
(2007?江苏)如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环.棒和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmg(k>1).断开轻绳,棒和环自由下落.假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失.棒在整个运动过程中始终保持竖直,空气阻力不计.求: (2011?桂林一模)如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环,棒和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力,大小为kmg(k>1).断开轻绳,棒和环自由下落,假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失,棒在整个运动过程中始终保持竖直,空气阻力不计,则( )
(2011?桂林一模)如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环,棒和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力,大小为kmg(k>1).断开轻绳,棒和环自由下落,假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失,棒在整个运动过程中始终保持竖直,空气阻力不计,则( ) 如图所示,一轻绳吊着质量为4m粗细均匀的棒,棒下端离地面高H,顶端套着一个细环,环的质量为m,棒与环相互间的最大静摩擦力等于滑动摩擦力4mg.断开轻绳,棒和环自由下落.落地后向上弹起的速度与落地时速度大小相等,不计空气阻力,运动过程中环与棒不分离.求:
如图所示,一轻绳吊着质量为4m粗细均匀的棒,棒下端离地面高H,顶端套着一个细环,环的质量为m,棒与环相互间的最大静摩擦力等于滑动摩擦力4mg.断开轻绳,棒和环自由下落.落地后向上弹起的速度与落地时速度大小相等,不计空气阻力,运动过程中环与棒不分离.求: