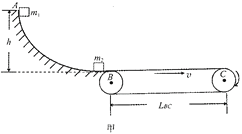
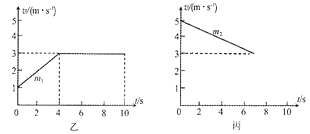
题目内容
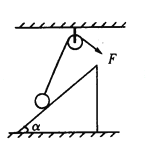
【题目】如图所示,质量为mA的滑块A和质量为mB的三角形滑块B叠放在倾角为θ的斜面体上,B的上表面水平.用水平向左的力F推斜面体,使它们从静止开始以相同的加速度a一起向左加速运动,由此可知( )
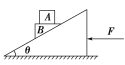
A.B对A的摩擦力大小等于mAa
B.斜面体与B之间一定有摩擦力
C.地面与斜面体之间一定有摩擦力
D.B对斜面体的压力可能等于(mA+mB) ![]()
【答案】AD
【解析】
以A研究对象,由牛顿第二定律求B对A的摩擦力大小.以AB整体为研究对象,由牛顿第二定律分析斜面对B是否有摩擦力.并分析地面和斜面间是否有摩擦力.对AB整体,由合成法分析斜面对B的支持力,再由牛顿第三定律求B对斜面的压力.
选AD.根据题述A和B随斜面体以相同的加速度a一起向左加速运动,由牛顿运动定律可知B对A的摩擦力f=mAa,选项A正确.把A、B看作整体分析受力,由牛顿运动定律可知当(mA+mB)gtan θ=(mA+mB)a时,即当斜面体运动的加速度a=gtan θ时,斜面体与B之间无摩擦力,斜面体对B的支持力等于(mA+mB)![]() ,由牛顿第三定律可知B对斜面体的压力等于(mA+mB)
,由牛顿第三定律可知B对斜面体的压力等于(mA+mB) ![]() ,选项B错误、D正确.把A、B和斜面体看作整体,若斜面体的质量为M,则当F=(M+mA+mB)a时,地面与斜面体之间没有摩擦力,当F>(M+mA+mB)a时,地面与斜面体之间有摩擦力,选项C错误.
,选项B错误、D正确.把A、B和斜面体看作整体,若斜面体的质量为M,则当F=(M+mA+mB)a时,地面与斜面体之间没有摩擦力,当F>(M+mA+mB)a时,地面与斜面体之间有摩擦力,选项C错误.

练习册系列答案
相关题目