题目内容
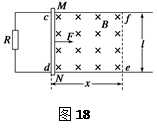
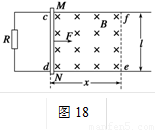
如图18所示，光滑的平行金属导轨水平放置，电阻不计，导轨间距为l，左侧接一阻值为R的电阻．区域cdef内存在垂直轨道平面向下的有界匀强磁场，磁场宽度为x．一质量为m、电阻为r的金属棒MN置于轨道上，与导轨垂直且接触良好，受到水平拉力F＝(0.5v＋0.4) N（v为某时刻金属棒运动的瞬时速度）的作用，从磁场的左边界由静止开始运动．已知l＝1 m，m＝1 kg，R＝0.3 Ω，r＝0.2 Ω，x＝0.8 m，如果测得电阻R两端的电压U随着时间是均匀增大的，那么：
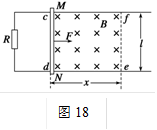
(1)分析并说明该金属棒在磁场中做何种运动；
(2)金属棒到达ef处的速度应该有多大；
(3)分析并求解磁感应强度B的大小．
（1）做初速度为零的匀加速直线运动（2）0.8m/s（3）0．5 T
解析:(1) （3分）因电阻两端的电压U随着时间t是均匀增大的，即：
而
，即
所以
，于是可以断定：金属棒必做初速度为零的匀加速直线运动
(2) （4分）设金属棒运动的加速度为a，在t＝0时v＝0，应用牛顿第二定律有
0．4 N＝ma
解得a＝0．4 m/s2
所以由v＝2ax，解得vef＝0.8m/s．
(3) （4分）根据题意，在金属棒运动的一般状态下，应用牛顿第二定律有：
(0．5v＋0．4)－
＝ma
又因为ma＝0.4为恒量，所以必有0.5＝
解得B＝0．5 T．
练习册系列答案
相关题目
