题目内容
某同学在做“探究单摆周期与摆长的关系”实验中:(1)为了减小测量周期的误差,摆球应选经过最______(填“高”或“低”)点的位置时开始计时并计数1次,且用秒表测得经过该位置n次的时间为t,则单摆的周期为______.
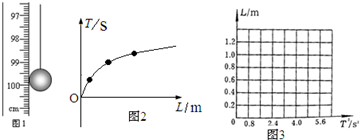
(2)用最小刻度为1mm的刻度尺测摆长,测量情况如图1所示,悬挂点在刻度尺的0mm处,从图中可知单摆的摆长L为______ m.
(3)为了寻找单摆周期与摆长的关系,在实验中要改变几次摆长L并测出相应的周期T,从而得出一组对应的T与L的数据,以L为横坐标,T为纵坐标得如图2所示图象.据此你猜测L与T可能有的关系是摆长L与______(填
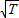 、T或T 2)成正比,要证实你的猜测,你应该以摆长L为横坐标,以它(你选定的
、T或T 2)成正比,要证实你的猜测,你应该以摆长L为横坐标,以它(你选定的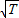 、T或T 2)为纵坐标作出图象;如果你作出的图象是______,那么你的猜测成立.
、T或T 2)为纵坐标作出图象;如果你作出的图象是______,那么你的猜测成立.(4)下表是“探究单摆周期与摆长的关系”实验的有关数据.
| 摆长L/m | 0.5100 | 0.6000 | 0.7900 | 1.0000 |
| 周期 | 2.0 | 2.4 | 3.2 | 4.8 |
②根据图象可知,当地的重力加速度g=______m/s2.
【答案】分析:(1)为了减小测量周期的误差,摆球应选经过最低点的位置时开始计时.根据全振动的次数,求出周期.
(2)刻度尺读数由准确值加估计值.要估计到0.01mm.
(3)根据图线的形状进行猜想,由数学知识根据解析式分析图象的形状.
(4)采用描点法作出图象,由单摆的周期公式得到g的表达式,再由数学知识求出g的值.
解答: 解:(1)摆球经过最低点的位置时速度最大,在相等的距离误差上引起的时间误差最小,测的周期误差最小.所以为了减小测量周期的误差,摆球应选经过最低点的位置时开始计时.由题分析可知,单摆全振动的次数为N=
解:(1)摆球经过最低点的位置时速度最大,在相等的距离误差上引起的时间误差最小,测的周期误差最小.所以为了减小测量周期的误差,摆球应选经过最低点的位置时开始计时.由题分析可知,单摆全振动的次数为N=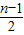 ,周期为T=
,周期为T=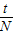 =
= ;
;
(2)单摆的摆长L为0.9950m.
(3)由图看出L-T图线是曲线,而且向右弯曲,根据数学知识可以猜想:摆长L与 T 2成正比,以摆长L为横坐标,以T 2为纵坐标作出的图象是过O点的直线.
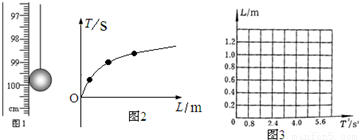
(4)采用描点法作出图象,如图所示.根据单摆的周期公式T=2 得,L=
得,L=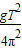 ,由图求出斜率k=
,由图求出斜率k= ,则
,则 =k=
=k= ,解得,g=9.86m/s2
,解得,g=9.86m/s2
故答案为:(1)低、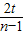 ;
;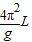
(2)0.9950(0.9948-0.9952);
(3)T 2、过O点的直线(或过O点的射线);
( 4)如图(最后一点应舍去) 9.86m/s2
点评:单摆测量时间的计时起点是平衡位置.根据单摆周期公式变形得到重力加速度的表达式再选择并分析图象的意义是常用的思路.
(2)刻度尺读数由准确值加估计值.要估计到0.01mm.
(3)根据图线的形状进行猜想,由数学知识根据解析式分析图象的形状.
(4)采用描点法作出图象,由单摆的周期公式得到g的表达式,再由数学知识求出g的值.
解答:
 解:(1)摆球经过最低点的位置时速度最大,在相等的距离误差上引起的时间误差最小,测的周期误差最小.所以为了减小测量周期的误差,摆球应选经过最低点的位置时开始计时.由题分析可知,单摆全振动的次数为N=
解:(1)摆球经过最低点的位置时速度最大,在相等的距离误差上引起的时间误差最小,测的周期误差最小.所以为了减小测量周期的误差,摆球应选经过最低点的位置时开始计时.由题分析可知,单摆全振动的次数为N=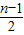 ,周期为T=
,周期为T=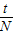 =
= ;
;(2)单摆的摆长L为0.9950m.
(3)由图看出L-T图线是曲线,而且向右弯曲,根据数学知识可以猜想:摆长L与 T 2成正比,以摆长L为横坐标,以T 2为纵坐标作出的图象是过O点的直线.
(4)采用描点法作出图象,如图所示.根据单摆的周期公式T=2
 得,L=
得,L=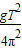 ,由图求出斜率k=
,由图求出斜率k= ,则
,则 =k=
=k= ,解得,g=9.86m/s2
,解得,g=9.86m/s2故答案为:(1)低、
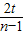 ;
;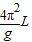
(2)0.9950(0.9948-0.9952);
(3)T 2、过O点的直线(或过O点的射线);
( 4)如图(最后一点应舍去) 9.86m/s2
点评:单摆测量时间的计时起点是平衡位置.根据单摆周期公式变形得到重力加速度的表达式再选择并分析图象的意义是常用的思路.

练习册系列答案
相关题目