题目内容
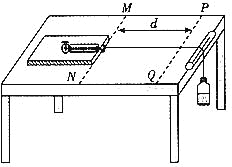
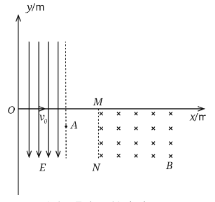
【题目】如图所示,![]() 的区域内存在着沿
的区域内存在着沿![]() 轴负方向的匀强电场E,E在
轴负方向的匀强电场E,E在![]() 轴方向区域足够大.有一个比荷为
轴方向区域足够大.有一个比荷为![]() 的带正电粒子(粒子重力不计) 从O点出发,以
的带正电粒子(粒子重力不计) 从O点出发,以![]() 的初速度沿
的初速度沿![]() 轴正方向射入电场,经过点A(
轴正方向射入电场,经过点A(![]() )离开电场.在第四象限垂直于
)离开电场.在第四象限垂直于![]() 轴的边界
轴的边界![]() 右侧的区域有磁感应强度为B的匀强磁场,M点的坐标为(
右侧的区域有磁感应强度为B的匀强磁场,M点的坐标为(![]() ).粒子进入磁场后,又穿过边界
).粒子进入磁场后,又穿过边界![]() 离开磁场.
离开磁场.
(1)求电场强度E的大小;
(2)求满足条件的磁感应强度B的最小值;
(3)若磁感应强度保持(2)中的最小值,将磁场区域改成圆形,为了使粒子能垂直击中![]() 轴上点G(
轴上点G(![]() ) ,求磁场区域的最小面积.
) ,求磁场区域的最小面积.
【答案】(1)![]() (2)1 T (3)
(2)1 T (3)![]()
【解析】
(1)粒子在电场中只受电场力作用做类平抛运动,故粒子做加速度
![]()
由粒子运动位移可得
![]()
![]()
由题意可知,![]()
解得电场强度
![]() .
.
(2)粒子运动轨迹如下图所示:
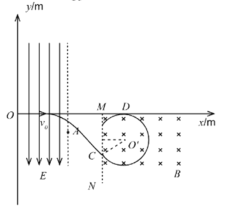
粒子离开电场进入磁场的过程不受力,做匀速直线运动,由(1)可得:粒子进入磁场时的水平分速度
![]()
竖直分速度
![]()
粒子在磁场中只受洛伦兹力作用,故粒子做匀速圆周运动,粒子在磁场中的运动速度
![]()
进入磁场时速度方向与竖直方向的角度![]() 满足
满足
![]() ,
,
故![]()
粒子离开电场进入磁场的过程中,竖直方向的位移
![]()
粒子进入磁场时的坐标为
(![]() )=(
)=(![]() )
)
由粒子进入磁场后,又穿过边界![]() 离开磁场,根据几何关系可得
离开磁场,根据几何关系可得
轨道半径
![]()
即![]()
根据洛伦兹力提供向心力可得
![]()
所以,磁感应强度![]() ,即满足条件的磁感应强度B的最小值为1 T.
,即满足条件的磁感应强度B的最小值为1 T.
(3)粒子运动轨迹如下所示:
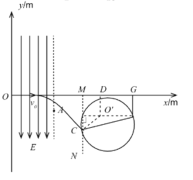
若磁感应强度保持(2)中的最小值,粒子在磁场中做圆周运动的轨道半径![]() ,使粒子能垂直击中
,使粒子能垂直击中轴上点G(
![]() ),则 要使粒子做匀速圆周运动的速度方向竖直向上时正好离开磁场区域;磁场区域为圆形,那么,当粒子进入磁场和离开磁场的两个点在磁场区域的一条直径上时磁场区域面积最小,故磁场区域的最小直径:
),则 要使粒子做匀速圆周运动的速度方向竖直向上时正好离开磁场区域;磁场区域为圆形,那么,当粒子进入磁场和离开磁场的两个点在磁场区域的一条直径上时磁场区域面积最小,故磁场区域的最小直径:
![]()
解得![]()
那么,磁场区域的最小面积
![]() .
.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目