题目内容
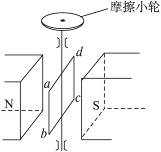
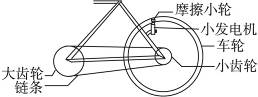
图17-1-18为演示用的手摇发电机模型,匀强磁场磁感应强度B=0.5T,线圈匝数N=50匝,每匝线圈面积为0.48 m2,转速为150 R/min.在匀速转动过程中,从图示位置线圈转过90°开始计时.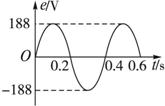
图17-1-18
(1)写出交流感应电动势瞬时值的表达式;
(2)画出e-t图线.
解析:从线圈平面经过中性面开始计时,则线圈在时间t内转过角度ωt,于是瞬时感应电动势e=Emsinωt,其中Em=2NBLv=NBSω.根据交流电的方程画图线时,最大值是正弦图线的峰值,由纵轴上的刻度值标出,交流电的角频率与正弦图线的周期相对应,ω=2π/T,而周期由时间轴上的刻度值标出.?
由题意知:?
N=50,B=0.5T,![]()
S=0.48 m2,e=Emsinωt,
Em=NBSω=50×0.5×0.48×5π V=188 V
所以(1)e=188sin5πt V?(2)T=2π/ω=0.4 s,e-t图线如下图所示.?


以下是一位同学做“探究形变与弹力的关系”的实验。
(1)下列的实验步骤是这位同学准备完成的,请你帮这位同学按操作的先后顺序,用字母排列出来是: 。
A.以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连结起来。
B.记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0
C.将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺
D.依次在弹簧下端挂上1个、2个、3个、4个……钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码
E、以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式.
F、解释函数表达式中常数的物理意义.
(2)下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据:
|
弹力(F/N) |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
|
弹簧原来长度(L0/cm) |
15 |
15 |
15 |
15 |
15 |
|
弹簧后来长度(L/cm) |
16.0 |
17.1 |
18.0 |
18.9 |
20 |
|
弹簧伸长量(x/cm) |
1.0 |
2.1 |
3.0 |
3.9 |
5.0 |
据上表的数据在右下图的坐标中作出F-x图线。
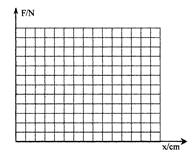
②写出曲线的函数表达式。(x用cm作单位):
③函数表达式中常数的物理意义:
以下是一位同学做“探究形变与弹力的关系”的实验。
(1)下列的实验步骤是这位同学准备完成的,请你帮这位同学按操作的先后顺序,用字母排列出来是: 。
A、以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连结起来。
B、记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0
C、将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺
D、依次在弹簧下端挂上1个、2个、3个、4个……钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码
E、以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式.
F、解释函数表达式中常数的物理意义.
(2)下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据:
|
弹力(F/N) |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
|
弹簧原来长度(L0/cm) |
15 |
15 |
15 |
15 |
15 |
|
弹簧后来长度(L/cm) |
16.0 |
17.1 |
18.0 |
18.9 |
20 |
|
弹簧伸长量(x/cm) |
1.0 |
2.1 |
3.0 |
3.9 |
5.0 |
①根据上表的数据在右下图的坐标中作出F-x图线。
②写出曲线的函数表达式。(x用cm作单位):
③函数表达式中常数的物理意义: