题目内容
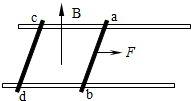 (2007?江苏模拟)如图所示,水平放置的光滑平行导轨的宽L=0.2m,轨道平面内有竖直向上的匀强磁场,磁感应强度B=0.5T,ab和cd棒均静止在导轨上,质量相等为m=0.1kg,电阻相等为R=0.5Ω.现用F=0.2N向右的水平恒力使ab棒由静止开始运动,经t=5s,ab棒的加速度a=1.37m/s2,则:
(2007?江苏模拟)如图所示,水平放置的光滑平行导轨的宽L=0.2m,轨道平面内有竖直向上的匀强磁场,磁感应强度B=0.5T,ab和cd棒均静止在导轨上,质量相等为m=0.1kg,电阻相等为R=0.5Ω.现用F=0.2N向右的水平恒力使ab棒由静止开始运动,经t=5s,ab棒的加速度a=1.37m/s2,则:(1)此时ab和cd两棒的速度vab、vcd各为多大?
(2)稳定时两棒的速度差是多少?
分析:(1)在两棒向右运动过程中,根据楞次定律与法拉第电磁感应定律,结合牛顿第二定律与动量定理,即可求解;
(2)由稳定状态可知,整体以稳定的速度差、相同的加速度一起向右做加速运动,根据牛顿第二定律,从而列式求解.
(2)由稳定状态可知,整体以稳定的速度差、相同的加速度一起向右做加速运动,根据牛顿第二定律,从而列式求解.
解答:解:(1)ab棒在外力F的作用下向右运动,从而产生感应电动势,使得ab棒受到水平向左的安培力,cd棒受到水平向右的安培力,两棒同时向右运动,均产生感应电动势,其回路的等效电动势
E等=Eab-Ecd=BLvab-BLvcd=BL(vab-vcd)=BL△v
根据牛顿第二定律有:F-F安=ma
又此时的安培力F安=BIL=
因为是非匀变速运动,故用动量定理有:
(F-F安)t=mvab-0
F安t=mvcd-0
得此时ab、cd两棒的速度分别为:vab=8.15m/s
vcd=1.85m/s.
(2)该题中的“稳定状态”又与前面两种情况不同,系统的合外力不为零且不变,“平衡状态”应该是它们的加速度相同,此时两棒速度不相同但保持“相对”稳定,所以整体以稳定的速度差、相同的加速度一起向右做加速运动.
用整体法有:F=2ma′
对cd棒用隔离法有:
=ma′
从而可得稳定时速度差△v=vab-vcd=10m/s.
答:(1)此时ab和cd两棒的速度分别为:vab=8.15m/s与vcd=1.85m/s;
(2)稳定时两棒的速度差是10m/s.
E等=Eab-Ecd=BLvab-BLvcd=BL(vab-vcd)=BL△v
根据牛顿第二定律有:F-F安=ma
又此时的安培力F安=BIL=
| B2L2(vab-vcd) |
| 2R |
因为是非匀变速运动,故用动量定理有:
(F-F安)t=mvab-0
F安t=mvcd-0
得此时ab、cd两棒的速度分别为:vab=8.15m/s
vcd=1.85m/s.
(2)该题中的“稳定状态”又与前面两种情况不同,系统的合外力不为零且不变,“平衡状态”应该是它们的加速度相同,此时两棒速度不相同但保持“相对”稳定,所以整体以稳定的速度差、相同的加速度一起向右做加速运动.
用整体法有:F=2ma′
对cd棒用隔离法有:
| B2L2(vab-vcd) |
| 2R |
从而可得稳定时速度差△v=vab-vcd=10m/s.
答:(1)此时ab和cd两棒的速度分别为:vab=8.15m/s与vcd=1.85m/s;
(2)稳定时两棒的速度差是10m/s.
点评:考查法拉第电磁感应定律与楞次定律、运用牛顿第二定律与动量定理,理解两棒的相对运动,区别稳定状态与平衡状态的不同.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
 (2007?江苏模拟)如图所示,截面为ABC的玻璃直角三棱镜放置在空气中,宽度均为d的紫、红两束光垂直照射三棱镜的一个直角边AB,在三棱镜的另一侧放置一平行于AB边的光屏,屏的距离远近可调,在屏上出现紫、红两条光带,可能是( )
(2007?江苏模拟)如图所示,截面为ABC的玻璃直角三棱镜放置在空气中,宽度均为d的紫、红两束光垂直照射三棱镜的一个直角边AB,在三棱镜的另一侧放置一平行于AB边的光屏,屏的距离远近可调,在屏上出现紫、红两条光带,可能是( ) (2007?江苏模拟)一轻弹簧的一端固定在地面上,另外一端与质量为m的物体相连,静止时如图所示,现在m上竖直向下施加一力F,下降h后无初速释放,则( )
(2007?江苏模拟)一轻弹簧的一端固定在地面上,另外一端与质量为m的物体相连,静止时如图所示,现在m上竖直向下施加一力F,下降h后无初速释放,则( ) (2007?江苏模拟)如图所示,质量为M的长平板车放在光滑的倾角为α的斜面上,车上站着一质量为m的人,若要平板车静止在斜面上,车上的人可以( )
(2007?江苏模拟)如图所示,质量为M的长平板车放在光滑的倾角为α的斜面上,车上站着一质量为m的人,若要平板车静止在斜面上,车上的人可以( )