题目内容
 光滑水平面上放着质量为mA=1kg的物块A和质量mB=2kg的物块B,A和B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧但与弹簧不拴接,用手挡住B不动,此时弹簧弹性势能EP=49J.在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示.放手后B向右运动,细绳在短暂时间内被拉断,之后B冲上固定在竖直平面内,底端与水平面光滑连接,半径R=0.5m的半圆形光滑轨道,已知B恰好能通过竖直轨道的最高点C,取g=10m/s2,求:
光滑水平面上放着质量为mA=1kg的物块A和质量mB=2kg的物块B,A和B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧但与弹簧不拴接,用手挡住B不动,此时弹簧弹性势能EP=49J.在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示.放手后B向右运动,细绳在短暂时间内被拉断,之后B冲上固定在竖直平面内,底端与水平面光滑连接,半径R=0.5m的半圆形光滑轨道,已知B恰好能通过竖直轨道的最高点C,取g=10m/s2,求:(1)绳拉断前瞬间B速度v的大小;
(2)绳拉断后瞬间B速度vB的大小;
(3)假设A在向右运动过程中没有碰到B,那么A能否到达轨道上与圆心等高的P点处?若能,求出A在P点处对轨道的压力;若不能,求出A能到达的最大高度.
【答案】分析:(1)绳断之间,弹簧已与A、B脱离,根据弹性势能全部转化为B的动能列出等式求解,
(2)在最高点C处,B所受重力恰好提供其做圆周运动的向心力,从绳断至到达最高点C,B物体机械能守恒列出等式求解.
(3)绳拉断的过程A和B组成的系统动量守恒列出等式,从绳断到A至P的过程中A的机械能守恒列出等式,在P点处,轨道对A的支持力提供其做圆周运动的向心力,根据牛顿第二定律求解.
解答:解:(1)绳断之间,弹簧已与A、B脱离,其弹性势能全部转化为B的动能
EP= m
m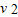
得v=7 m/s
(2)在最高点C处,B所受重力恰好提供其做圆周运动的向心力
mBg=mB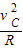
从绳断至到达最高点C,B物体机械能守恒
 mB
mB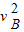 =2mBgR+
=2mBgR+ mB
mB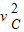
得vB=5m/s
(3)绳拉断的过程A和B组成的系统动量守恒
mBv=mBvB+mAvA
设A到达P点时的速度为vAP,从绳断到A至P的过程中A的机械能守恒
 mA
mA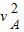 =mAgR+
=mAgR+ mA
mA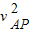
得vAP=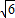 m/s>0,A能到达P点,在P点处,轨道对A的支持力提供其做圆周运动的向心力
m/s>0,A能到达P点,在P点处,轨道对A的支持力提供其做圆周运动的向心力
FN=mA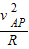 =12N
=12N
由牛顿第三定律可知,A对轨道的压力FN=FN′=12N,方向水平向右
答:(1)绳拉断前瞬间B速度v的大小是7 m/s;
(2)绳拉断后瞬间B速度vB的大小是5m/s;
(3)A能到达P点,出A在P点处对轨道的压力是12N,方向水平向右.
点评:该题考查了多个知识点.我们首先要清楚物体的运动过程,要从题目中已知条件出发去求解问题.
其中应用动能定理时必须清楚研究过程和过程中各力做的功.应用动量定理和动量守恒定律时要规定正方向,要注意矢量的问题.
(2)在最高点C处,B所受重力恰好提供其做圆周运动的向心力,从绳断至到达最高点C,B物体机械能守恒列出等式求解.
(3)绳拉断的过程A和B组成的系统动量守恒列出等式,从绳断到A至P的过程中A的机械能守恒列出等式,在P点处,轨道对A的支持力提供其做圆周运动的向心力,根据牛顿第二定律求解.
解答:解:(1)绳断之间,弹簧已与A、B脱离,其弹性势能全部转化为B的动能
EP=
 m
m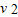
得v=7 m/s
(2)在最高点C处,B所受重力恰好提供其做圆周运动的向心力
mBg=mB
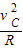
从绳断至到达最高点C,B物体机械能守恒
 mB
mB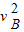 =2mBgR+
=2mBgR+ mB
mB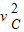
得vB=5m/s
(3)绳拉断的过程A和B组成的系统动量守恒
mBv=mBvB+mAvA
设A到达P点时的速度为vAP,从绳断到A至P的过程中A的机械能守恒
 mA
mA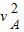 =mAgR+
=mAgR+ mA
mA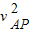
得vAP=
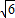 m/s>0,A能到达P点,在P点处,轨道对A的支持力提供其做圆周运动的向心力
m/s>0,A能到达P点,在P点处,轨道对A的支持力提供其做圆周运动的向心力FN=mA
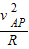 =12N
=12N 由牛顿第三定律可知,A对轨道的压力FN=FN′=12N,方向水平向右
答:(1)绳拉断前瞬间B速度v的大小是7 m/s;
(2)绳拉断后瞬间B速度vB的大小是5m/s;
(3)A能到达P点,出A在P点处对轨道的压力是12N,方向水平向右.
点评:该题考查了多个知识点.我们首先要清楚物体的运动过程,要从题目中已知条件出发去求解问题.
其中应用动能定理时必须清楚研究过程和过程中各力做的功.应用动量定理和动量守恒定律时要规定正方向,要注意矢量的问题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 如图,在光滑水平面上放着质量分别为m和2m的A、B两个物块,现用外力缓慢向左推B使弹簧压缩,此过程中推力做功W.然后撤去外力,则( )
如图,在光滑水平面上放着质量分别为m和2m的A、B两个物块,现用外力缓慢向左推B使弹簧压缩,此过程中推力做功W.然后撤去外力,则( ) (2008?天津)光滑水平面上放着质量mA=lkg的物块A与质量mB=2kg的物块B,A与B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧(弹簧与A、B均不拴接),用手挡住B不动,此时弹簧弹性势能EP=49J.在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示.放手后B向右运动,绳在短暂时间内被拉断,之后B冲上与水平面相切的竖直半圆光滑轨道,其半径R=0.5m,B恰能到达最高点C.取g=l0m/s2,求
(2008?天津)光滑水平面上放着质量mA=lkg的物块A与质量mB=2kg的物块B,A与B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧(弹簧与A、B均不拴接),用手挡住B不动,此时弹簧弹性势能EP=49J.在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示.放手后B向右运动,绳在短暂时间内被拉断,之后B冲上与水平面相切的竖直半圆光滑轨道,其半径R=0.5m,B恰能到达最高点C.取g=l0m/s2,求 如图,在光滑水平面上放着质量分别为m和2m的A、B两个物块,现用外力缓慢向左推B使弹簧压缩,此过程中推力做功W.然后撤去外力,则( )
如图,在光滑水平面上放着质量分别为m和2m的A、B两个物块,现用外力缓慢向左推B使弹簧压缩,此过程中推力做功W.然后撤去外力,则( )