题目内容
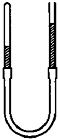 如图所示,下端用橡皮管连接的两根粗细相同的玻璃管竖直放置,右管开口,左管内被封闭气柱长20cm,水银面比右管低15cm,大气压强为 75cmHg.现保持左管不动,为了使两管内水银面一样高,则
如图所示,下端用橡皮管连接的两根粗细相同的玻璃管竖直放置,右管开口,左管内被封闭气柱长20cm,水银面比右管低15cm,大气压强为 75cmHg.现保持左管不动,为了使两管内水银面一样高,则(1)右管应向上还是向下移动?
(2)两边液面相平时,气柱长度为多少?
(3)右管管口移动的距离是多少?
分析:(1)图中左管中封闭气体的压强大于大气压,当两管内水银面相平时,封闭气体的压强等于大气压,而气体发生了等温变化,根据玻意耳定律进行分析.
(2)分别列出初态和末态封闭气体的压强、体积,由根据玻意耳定律列式可求出两边液面相平时气柱长度.
(3)根据几何关系求右管管口移动的距离.
(2)分别列出初态和末态封闭气体的压强、体积,由根据玻意耳定律列式可求出两边液面相平时气柱长度.
(3)根据几何关系求右管管口移动的距离.
解答:解:(1)两管内水银面一样高,左管中空气的压强减小,由玻意耳定律知,气体的体积要增大,右管必须向下移动.
(2)左管中气体,初态:p1=75+15=90cmHg,V1=20S
末态:p2=75 cmHg V2=L2S
由P1V1=p1V2得
90×20S=75×L2S
解得 L2=24cm
(3)设右管管口向下移动距离为x,
则
=4
解得 x=23cm
答:
(1)右管应向下移动.
(2)两边液面相平时,气柱长度为24cm.
(3)右管管口移动的距离是23cm.
(2)左管中气体,初态:p1=75+15=90cmHg,V1=20S
末态:p2=75 cmHg V2=L2S
由P1V1=p1V2得
90×20S=75×L2S
解得 L2=24cm
(3)设右管管口向下移动距离为x,
则
| x-15 |
| 2 |
解得 x=23cm
答:
(1)右管应向下移动.
(2)两边液面相平时,气柱长度为24cm.
(3)右管管口移动的距离是23cm.
点评:此题考查玻意耳定律的应用,确定初末状态的参量是解题的关键.

练习册系列答案
相关题目
 分享到
分享到- QQ空间
- 新浪微博
- 百度搜藏
- 人人网
- 腾讯微博
- 开心网
- 腾讯朋友
- 百度空间
- 豆瓣网
- 搜狐微博
- MSN
- QQ收藏
- 我的淘宝
- 百度贴吧
- 搜狐白社会
- 更多...
百度分享
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,用下面的方法测量它匀速转动时的角速度。
实验器材:电磁打点计时器、米尺、纸带、复写纸片。
实验步骤:
(1)如图1所示,将电磁打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔后,固定在待测圆盘的侧面上,使得圆盘转动时,纸带可以卷在圆盘侧面上。
(2)启动控制装置使圆盘转动,同时接通电源,打点计时器开始打点。
(3)经过一段时间,停止转动和打点,取下纸带,进行测量。
① 由已知量和测得量表示的角速度的表达式为ω= 。式中各量的意义是:
.
② 某次实验测得圆盘半径r=5.50×10-2m,得到纸带的一段如图2所示,求得角速度为 。
(1) (2)6.8/s。 |
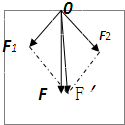 (1)在“验证力的平行四边形定则”实验中,用两个弹簧测力计分别钩住细绳套,互成角度地拉橡皮条,使它伸长到某一位置O点,这一步操作中必须记录的是( )
(1)在“验证力的平行四边形定则”实验中,用两个弹簧测力计分别钩住细绳套,互成角度地拉橡皮条,使它伸长到某一位置O点,这一步操作中必须记录的是( ) [1]、(11分)某学生利用“研究匀变速直线运动”的实验装置来测量一个质量m=50g的重锤下落时的加速度值,该学生将重锤固定在纸带下端,让纸带穿过打点计时器,实验装置如图所示.
[1]、(11分)某学生利用“研究匀变速直线运动”的实验装置来测量一个质量m=50g的重锤下落时的加速度值,该学生将重锤固定在纸带下端,让纸带穿过打点计时器,实验装置如图所示.

 在做“验证力的平行四边形定则”的实验时:
在做“验证力的平行四边形定则”的实验时: