题目内容
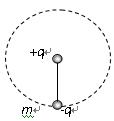
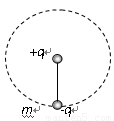
 M是一长为L的竖直放置的绝缘挡板,N是一块同样长的与水平面成45°角且与M相对放置的绝缘挡板,它们的底边保持平行.在M板正中央O点有一个质子速度V0对着N板水平射出,首次击中N板的点与O点相距为d.设所有碰撞均无能量损失.在整个装置中有水平向右的匀强磁场,磁感应强度为B,假设质子最后一次碰撞发生在N板的正边缘处,试求:
M是一长为L的竖直放置的绝缘挡板,N是一块同样长的与水平面成45°角且与M相对放置的绝缘挡板,它们的底边保持平行.在M板正中央O点有一个质子速度V0对着N板水平射出,首次击中N板的点与O点相距为d.设所有碰撞均无能量损失.在整个装置中有水平向右的匀强磁场,磁感应强度为B,假设质子最后一次碰撞发生在N板的正边缘处,试求:(1)挡板长L应满足什么条件?
(2)质子在两板间的运动时间.
分析:(1)根据洛伦兹力提供向心力,结合牛顿第二定律,与几何关系,即可求解;
(2)由运动学公式,求出直线运动,根据周期公式与圆心角的关系,求出圆周运动时间,最后两者之和为质子在两板间的运动时间.
(2)由运动学公式,求出直线运动,根据周期公式与圆心角的关系,求出圆周运动时间,最后两者之和为质子在两板间的运动时间.
解答:解:(1)设碰撞n次,则有:
=2nR;
洛伦兹力提供向心力,由牛顿第二定律,则有:Bev0=m
,
由上两式,联立解得:L=
(n=1,2,3,…)
(2)直线运动时间:t1=
圆运动时间:t2=n
总运动时间:t=t1+t2=
+
答:(1)挡板长L应满足:L=
(n=1,2,3,…);
(2)质子在两板间的运动时间
+
.
| L |
| 2 |
洛伦兹力提供向心力,由牛顿第二定律,则有:Bev0=m
| ||
| R |
由上两式,联立解得:L=
| 4nmv0 |
| eB |
(2)直线运动时间:t1=
| (2n+1)d |
| V0 |
圆运动时间:t2=n
| πR |
| eB |
总运动时间:t=t1+t2=
| (2n+1)d |
| V0 |
| πnmV0 |
| e2B2 |
答:(1)挡板长L应满足:L=
| 4nmv0 |
| eB |
(2)质子在两板间的运动时间
| (2n+1)d |
| v0 |
| πnmv0 |
| e2B2 |
点评:考查粒子在磁场中做匀速圆周运动,掌握牛顿第二定律与运动学公式的应用,注意学会求圆周运动的时间.

练习册系列答案
相关题目
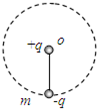 如图所示,一长为L的绝缘细线下端系质量为m的金属小球,并带有-q的电荷量,在细线的悬点o处放一带电荷量为+q的点电荷.要使金属球能在竖直平面内做完整的圆周运动,求:
如图所示,一长为L的绝缘细线下端系质量为m的金属小球,并带有-q的电荷量,在细线的悬点o处放一带电荷量为+q的点电荷.要使金属球能在竖直平面内做完整的圆周运动,求: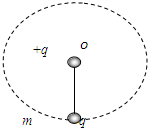 如图所示,一长为L的绝缘细线下端系质量为m的金属小球,带-q的电荷量,在细线的悬点O处放一带电荷量为+q的点荷.要使金属球能在竖直平面内做完整的圆周运动.
如图所示,一长为L的绝缘细线下端系质量为m的金属小球,带-q的电荷量,在细线的悬点O处放一带电荷量为+q的点荷.要使金属球能在竖直平面内做完整的圆周运动.