题目内容
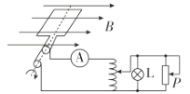
【题目】如图甲所示,两根完全相同的光滑导轨固定在水平面上,每根导轨均由两段与水平面成![]() 的长直导轨和一段圆弧导轨平滑连接而成,导轨两端均连接电阻,阻值
的长直导轨和一段圆弧导轨平滑连接而成,导轨两端均连接电阻,阻值![]() 。导轨间距
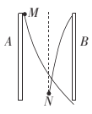
。导轨间距![]() 在右侧导轨所在斜面的矩形区域
在右侧导轨所在斜面的矩形区域![]() 内分布有垂直斜面向上的磁场,磁场上下边界
内分布有垂直斜面向上的磁场,磁场上下边界![]() 、
、![]() 的距离
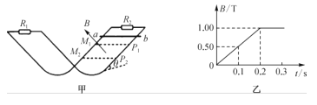
的距离![]() 。磁感应强度大小随时间的变化规律如图乙所示。
。磁感应强度大小随时间的变化规律如图乙所示。![]() 时刻,在右侧导轨斜面上与
时刻,在右侧导轨斜面上与![]() 距离
距离![]() 处,有一根阻值
处,有一根阻值![]() 的金属棒ab垂直于导轨由静止释放,恰好匀速通过整个磁场区域,重力加速度g取
的金属棒ab垂直于导轨由静止释放,恰好匀速通过整个磁场区域,重力加速度g取![]() ,导轨电阻不计。求:
,导轨电阻不计。求:
(1)金属棒ab在磁场中运动的速度大小v;
(2)在![]() 时刻和
时刻和![]() 时刻电阻R1的电功率之比;
时刻电阻R1的电功率之比;
(3)金属棒ab从静止释放到不再进人磁场区域的过程中,电阻![]() 产生的总热量
产生的总热量![]() 。
。
【答案】(1)1m/s (2)4:1(3)0.01J
【解析】
(1)根据动能定理可得
![]()
解![]()
(2)金属棒从释放到运动至![]() 的时间
的时间
![]()
在![]() 时,金属棒还没有进入磁场,有
时,金属棒还没有进入磁场,有
![]()
此时![]() 与金属棒并联后再与
与金属棒并联后再与![]() 串联,则
串联,则
![]()
根据欧姆定律可得![]()
由图乙可知,![]() 后磁场保持不变,ab经过磁场的时间
后磁场保持不变,ab经过磁场的时间
![]()
故在![]() 时,ab还在磁场中运动,电动势
时,ab还在磁场中运动,电动势
![]()
此时![]() 和
和![]() 并联
并联
![]()
![]() 路端电压
路端电压
![]()
根据电功率的计算公式![]() 可得,在
可得,在![]() 时刻和
时刻和![]() 时刻电阻
时刻电阻![]() 的电功率之比:
的电功率之比:
![]()
(3)设ab的质量为m,ab在磁场中运动时,通过ab的电流为
![]()
ab受到的安培力为
![]()
![]()
解得![]()
在![]() 时间内,
时间内,![]() 两端电压
两端电压![]() ,产生的热量
,产生的热量
![]()
ab最终将在![]() 下方的轨道区域往返运动,到
下方的轨道区域往返运动,到![]() 处的速度为零,根据功能关系可得在
处的速度为零,根据功能关系可得在![]() 后整个电路最终产生的热量
后整个电路最终产生的热量
![]()
由电路关系可得![]() 产生的热量
产生的热量
![]()
故![]() 产生的总热量
产生的总热量
![]()

练习册系列答案
相关题目