题目内容
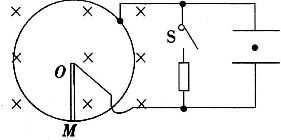 半径为a的圆环电阻不计,放置在垂直于纸面向里,磁感应强度为B的匀强磁场中,环内有一导体棒电阻为r,可以绕环匀速转动,将电阻R、开关S连接在环和棒的O端,将电容器极板水平放置,并联在R和开关S两端,如图所示.
半径为a的圆环电阻不计,放置在垂直于纸面向里,磁感应强度为B的匀强磁场中,环内有一导体棒电阻为r,可以绕环匀速转动,将电阻R、开关S连接在环和棒的O端,将电容器极板水平放置,并联在R和开关S两端,如图所示.(1)开关S断开,极板间有一电荷量为q、质量为m的带正电粒子恰好静止,试判断OM的转动方向和角速度的大小.
(2)当S闭合时,该带电粒子以
| 1 | 4 |
分析:(1)开关S断开:粒子带正电,且恰好静止,受到的电场力与重力平衡,可判断出电容器极板所带电荷的电性,再由右手定则判断OM转动方向.
粒子受力平衡,由平衡条件列式,得出电容器板间电压U,即等于OM产生的感应电动势,由转动切割的感应电动势公式E=
Ba2ω求角速度ω.
(2)开关S闭合:电容器的电压减小,带电粒子所受的电场力减小,向下做匀加速运动,由牛顿第二定律和E=
求出此时板间电压U′,再由电路的连接关系求R是r的几倍.
粒子受力平衡,由平衡条件列式,得出电容器板间电压U,即等于OM产生的感应电动势,由转动切割的感应电动势公式E=
| 1 |
| 2 |
(2)开关S闭合:电容器的电压减小,带电粒子所受的电场力减小,向下做匀加速运动,由牛顿第二定律和E=
| U′ |
| d |
解答:解:(1)由于粒子带正电,恰好静止在电容器中,则电容器上极板带负电,由右手定则判断可知,OM应绕O沿逆时针方向转动.
粒子受力平衡,有mg=q
当S断开时,U=E
又OM产生的感应电动势为 E=
Ba2ω
解得ω=
(2)当S闭合时,根据牛顿第二定律得:mg-q
=m?
又U′=
R
解得
=3
答:
(1)开关S断开,极板间有一电荷量为q、质量为m的带正电粒子恰好静止,OM的转动方向为逆时针,角速度的大小为
.
(2)当S闭合时,该带电粒子以
g的加速度向下运动,则R是r的3倍.
粒子受力平衡,有mg=q
| U |
| d |
当S断开时,U=E
又OM产生的感应电动势为 E=
| 1 |
| 2 |
解得ω=
| 2mgd |
| qBa2 |
(2)当S闭合时,根据牛顿第二定律得:mg-q
| U′ |
| d |
| g |
| 4 |
又U′=
| E |
| R+r |
解得
| R |
| r |
答:
(1)开关S断开,极板间有一电荷量为q、质量为m的带正电粒子恰好静止,OM的转动方向为逆时针,角速度的大小为
| 2mgd |
| qBa2 |
(2)当S闭合时,该带电粒子以
| 1 |
| 4 |
点评:本题是电磁感应中电路问题,关键要掌握转动切割的感应电动势公式 E=
Ba2ω及欧姆定律等等基本知识.
| 1 |
| 2 |

练习册系列答案
相关题目
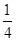 g的加速度向下运动,则R是r的几倍?
g的加速度向下运动,则R是r的几倍?
 g的加速度向下运动,则R是r的几倍?
g的加速度向下运动,则R是r的几倍?