题目内容
 如图所示,截面为直角三角形ABC,∠B=30°,斜边AB=a.棱镜材料的折射率为n=
如图所示,截面为直角三角形ABC,∠B=30°,斜边AB=a.棱镜材料的折射率为n=| 2 |
(1)光从棱镜第一次射出时的折射角;
(2)光从棱镜第一次射出时的射出点与B点间的距离.
分析:(1)先根据临界角公式sinC=
求出玻璃砖的临界角C.根据几何知识确定光线在AB或BC面上入射角,判断在这两个面上能否发生全反射,画出光路图,由折射定律求解光从棱镜第一次射出时的折射角.
(2)由几何知识求出光从棱镜第一次射出时的射出点与B点间的距离.
| 1 |
| n |
(2)由几何知识求出光从棱镜第一次射出时的射出点与B点间的距离.
解答: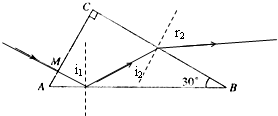 解:(1)设玻璃砖的临界角为C.则有sinC=
解:(1)设玻璃砖的临界角为C.则有sinC=
=
得:C=45°
由几何知识知:光线在AB面上的入射角 i1=60°>C,所以光线在AB上发生全反射.
根据反射定律和几何关系得知光线在BC面上的入射角 i2=30°<C,可知光线将从BC面上射出玻璃砖.
设光从棱镜第一次射出时的折射角为r2.
则有:n=
得:sinr2=nsini2=
×sin30°=
,
r2=45°.
(2)根据几何知识得:AD=
=2AM=
BD=AB-AD=a-
=
a
故EB=
=
=
a
答:(1)光从棱镜第一次射出时的折射角是45°;
(2)光从棱镜第一次射出时的射出点与B点间的距离是
a.
 解:(1)设玻璃砖的临界角为C.则有sinC=
解:(1)设玻璃砖的临界角为C.则有sinC=| 1 |
| n |
| 1 | ||
|
得:C=45°
由几何知识知:光线在AB面上的入射角 i1=60°>C,所以光线在AB上发生全反射.
根据反射定律和几何关系得知光线在BC面上的入射角 i2=30°<C,可知光线将从BC面上射出玻璃砖.
设光从棱镜第一次射出时的折射角为r2.
则有:n=
| sinr2 |
| sini2 |
得:sinr2=nsini2=
| 2 |
| ||
| 2 |
r2=45°.
(2)根据几何知识得:AD=
| AM |
| cos60° |
| a |
| 4 |
BD=AB-AD=a-
| a |
| 4 |
| 3 |
| 4 |
故EB=
| ||
| cos30° |
| ||||
|
| ||
| 4 |
答:(1)光从棱镜第一次射出时的折射角是45°;
(2)光从棱镜第一次射出时的射出点与B点间的距离是
| ||
| 4 |
点评:本题是折射定律与几何知识的综合应用,正确判断光线能否发生全反射是关键,要掌握全反射的条件:光从光密介质射入光疏介质,入射角大于临界角,灵活运用几何知识解决物理问题.

练习册系列答案
相关题目
 如图所示,截面为直角三角形的玻璃棱镜置于真空中,已知∠A=60°,∠C=90°;一束极细的光于AC边的中点F处垂直AC面入射,AC=2
如图所示,截面为直角三角形的玻璃棱镜置于真空中,已知∠A=60°,∠C=90°;一束极细的光于AC边的中点F处垂直AC面入射,AC=2 如图所示,截面为直角三角形的区域内,有一个具有理想边界的匀强磁场,磁场方向垂直纸面向里,磁感应强度大小为B,三角形区域的ab边长为L,θ=30°.一个电子从ab边界外侧由ab边中点处与ab成30°角垂直于磁场方向射入磁场内,已知电子的电荷量为e,质量为m,为使电子能从ac边射出,电子的入射速度v0的大小应该满足什么条件?
如图所示,截面为直角三角形的区域内,有一个具有理想边界的匀强磁场,磁场方向垂直纸面向里,磁感应强度大小为B,三角形区域的ab边长为L,θ=30°.一个电子从ab边界外侧由ab边中点处与ab成30°角垂直于磁场方向射入磁场内,已知电子的电荷量为e,质量为m,为使电子能从ac边射出,电子的入射速度v0的大小应该满足什么条件? cm,玻璃的折射率为n=
cm,玻璃的折射率为n= ,光在真空的速度为
,光在真空的速度为 m/s 求:
m/s 求:
 cm,玻璃的折射率为n=
cm,玻璃的折射率为n= ,光在真空的速度为
,光在真空的速度为 m/s 求:
m/s 求: