题目内容
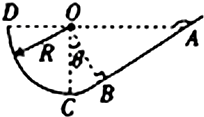 如图所示,竖直面内有一粗糙斜面AB,BCD部分是一个光滑的圆弧面,C为圆弧的最低点,AB正好是圆弧在B点的切线,圈心点O与A、D点在同一高度,∠OAB=37°,圆弧面的半径R=3.6m,一小滑块质量m=5kg,与A斜面间的动摩擦因数μ=0.45,将滑块由A点静止释放,求在以后的运动中(sin37°=0.6,cos37°=0.8)
如图所示,竖直面内有一粗糙斜面AB,BCD部分是一个光滑的圆弧面,C为圆弧的最低点,AB正好是圆弧在B点的切线,圈心点O与A、D点在同一高度,∠OAB=37°,圆弧面的半径R=3.6m,一小滑块质量m=5kg,与A斜面间的动摩擦因数μ=0.45,将滑块由A点静止释放,求在以后的运动中(sin37°=0.6,cos37°=0.8)(1)滑块在AB段上运动的总路程;
(2)在滑块运动过程中,C点受到的压力的最大值和最小值.
分析:(1)由几何知识得知,斜面的倾角等于30°.物体从A点无初速度滑下后,由于克服摩擦力做功,物体在斜面上运动时机械能不断减小,到达的最大高度越来越小,最终在BE圆弧上来回运动,到达B点的速度为零.物体在斜面上运动时摩擦力大小为μmgcosθ,总是做负功,滑动摩擦力做的总功与总路程成正比,根据动能定理求解总路程.
(2)当物体第一次经过C点时,速度最大,对C点的压力最大,当最后稳定后,物体在BE之间运动时,经过C点时速度最小,物体对C点的压力最小,根据动能定理求出最大速度和最小速度,再由牛顿运动定律求解最大压力和最小压力.
(2)当物体第一次经过C点时,速度最大,对C点的压力最大,当最后稳定后,物体在BE之间运动时,经过C点时速度最小,物体对C点的压力最小,根据动能定理求出最大速度和最小速度,再由牛顿运动定律求解最大压力和最小压力.
解答:解:(1)由于滑块在AB段受摩擦力作用,则滑块往复振荡的高度将越来越低,最终以B为最高点在光滑的圆弧段往复运动,设滑块在AB上运动的总路程为s.
滑块在AB段上受摩擦力,f=μFN=μmgcosθ
从A点出发到最终以B点为最高点振荡,根据能量守恒有:△Ep=fs
即:mgRcosθ=fs
解得s=
=8m
(2)滑块第一次过C点时,速度最大,设为v1,分析受力知此时小球受轨道支持力最在,设在Fmax,从A到C,根据动能定理有:mgR-flAB=
m
根据受力以及向心力公式知:Fmax-mg=
联立两式并代入数据得:Fmax=102N
当滑块以B为最高点往复运动的过程中过C点时速度最小,设为v2.
此时小球受轨道支持力也最小,设为Fmin
从B到C,根据动能定理有:mgR(1-cosθ)=
m
根据受力及向心力公式有:Fmin-mg=
联立两式并代入数据得:Fmin=70N
根据牛顿第三定律可知C点受到的压力最大值为102N,最小值为70N
答:(1)滑块在AB段上运动的总路程为8m;
(2)在滑块运动过程中,C点受到的压力的最大值为102N,最小值70N.
滑块在AB段上受摩擦力,f=μFN=μmgcosθ
从A点出发到最终以B点为最高点振荡,根据能量守恒有:△Ep=fs
即:mgRcosθ=fs
解得s=
| mgRcosθ |
| f |
(2)滑块第一次过C点时,速度最大,设为v1,分析受力知此时小球受轨道支持力最在,设在Fmax,从A到C,根据动能定理有:mgR-flAB=
| 1 |
| 2 |
| v | 2 1 |
根据受力以及向心力公式知:Fmax-mg=
m
| ||
| R |
联立两式并代入数据得:Fmax=102N
当滑块以B为最高点往复运动的过程中过C点时速度最小,设为v2.
此时小球受轨道支持力也最小,设为Fmin
从B到C,根据动能定理有:mgR(1-cosθ)=
| 1 |
| 2 |
| v | 2 2 |
根据受力及向心力公式有:Fmin-mg=
m
| ||
| R |
联立两式并代入数据得:Fmin=70N
根据牛顿第三定律可知C点受到的压力最大值为102N,最小值为70N
答:(1)滑块在AB段上运动的总路程为8m;
(2)在滑块运动过程中,C点受到的压力的最大值为102N,最小值70N.
点评:本题是动能定理与牛顿运动定律的综合应用,关键是分析物体的运动过程,抓住滑动摩擦力做功与路程有关这一特点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
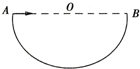 如图所示,竖直面内有一个半圆形轨道,AB为水平直径,O为圆心,将一些半径远小于轨道半径的小球从A点以不同的初速度水平向右抛出,若不计空气阻力,在小球从抛出到碰到轨道这个过程中,下列说法正确的是( )
如图所示,竖直面内有一个半圆形轨道,AB为水平直径,O为圆心,将一些半径远小于轨道半径的小球从A点以不同的初速度水平向右抛出,若不计空气阻力,在小球从抛出到碰到轨道这个过程中,下列说法正确的是( )| A、初速度大的小球运动时间长 | B、小球落到落在半圆形轨道的瞬间,速度方向沿半径方向 | C、落在圆形轨道最低点的小球运动时间最长 | D、初速度不同的小球运动时间不可能相同 |
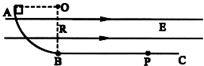 如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)
如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2) 如图所示,竖直面内有一个半径为R=0.2m的光滑半圆形轨道固定在地面上,水平地面与轨道相切于B点.小球以υ0=3m/s的速度从最低点B进入轨道,关于小球落地点和轨道最低点B的距离,某同学做如下计算:
如图所示,竖直面内有一个半径为R=0.2m的光滑半圆形轨道固定在地面上,水平地面与轨道相切于B点.小球以υ0=3m/s的速度从最低点B进入轨道,关于小球落地点和轨道最低点B的距离,某同学做如下计算: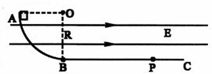 (2009?天津模拟)如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)
(2009?天津模拟)如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)