题目内容
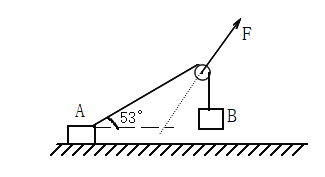
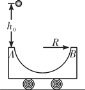
【题目】如图所示,质量为m的半圆轨道小车静止在光滑的水平地面上,其水平直径AB长度为2R,现将质量也为m的小球从距A点正上方h0高处由静止释放,然后由A点经过半圆轨道后从B冲出,在空中能上升的最大高度为![]() h0(不计空气阻力),则( )
h0(不计空气阻力),则( )
A.小球和小车组成的系统动量守恒
B.小车向左运动的最大距离为R
C.小球离开小车后做斜上抛运动
D.小球第二次冲过A能上升的最大高度![]() h0<h<
h0<h<![]() h0
h0
【答案】BD
【解析】
A.小球与小车组成的系统在水平方向所受的合外力为零,水平方向系统动量守恒。由于小球有竖直分加速度,所以系统所受的合外力不为零,系统动量不守恒,故A错误;
B.系统水平方向动量守恒,以向右为正方向,在水平方向,由动量守恒定律得
![]()
即
![]()
解得,小车的最大位移
![]()
故B正确;
C.小球与小车组成的系统在水平方向动量守恒,小球由A点离开小车时系统水平方向动量为零,小球与小车水平方向速度为零,小球离开小车后做竖直上抛运动,故C错误;
D.小球第一次车中运动过程中,由动能定理得
![]()
Wf为小球克服摩擦力做功大小,解得
![]()
即小球第一次在车中滚动损失的机械能为![]() ,由于小球第二次在车中滚动时,对应位置处速度变小,因此小车给小球的弹力变小,摩擦力变小,摩擦力做功小于
,由于小球第二次在车中滚动时,对应位置处速度变小,因此小车给小球的弹力变小,摩擦力变小,摩擦力做功小于![]() ,机械能损失小于
,机械能损失小于![]() ,因此小球再次离开小车时,能上升的高度大于
,因此小球再次离开小车时,能上升的高度大于
![]()
而小于![]() ,即
,即
![]()
故D正确。
故选BD。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目