题目内容
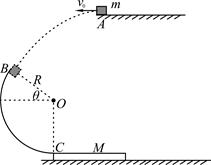
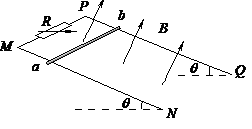
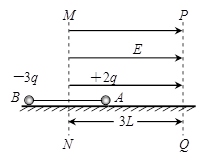
)一绝缘“?”形杆由两段相互平行的足够长的水平直杆PQ、MN和一半径为R的光滑半圆环MAP组成,固定在竖直平面内,其中MN杆是光滑的,PQ杆是粗糙的.现将一质量为m的带正电荷的小环套在MN杆上,小环所受的电场力为重力的 .
.
(1)若将小环由D点静止释放,则刚好能到达P点,求DM间的距离;
(2)若将小环由M点右侧5R处静止释放,设小环与PQ杆间的动摩擦因数为μ,小环所受最大静摩擦力与滑动摩擦力大小相等,求小环在整个运动过程中克服摩擦力所做的功.
(1) DM间的距离j4R;(2)若μ≥ ,整个运动过程中克服摩擦力所做的功为
,整个运动过程中克服摩擦力所做的功为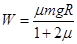
若μ< ,克服摩擦力做功
,克服摩擦力做功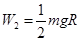
解析试题分析: (1)小球刚好到达P点时,速度为零,对小球从D点到P点过程,由动能定理得
qEx-2mgR=0-0
又由题意,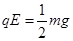
联立解得,x=4R
若μ≥ ,则μmg≥qE.
,则μmg≥qE.
设小球到达P点左侧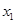 静止,由动能定理得
静止,由动能定理得
qE(5R-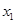 )-mg?2R-f
)-mg?2R-f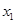 =0
=0
又f=μN=μmg
联立解得,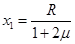
所以整个运动过程中克服摩擦力所做的功为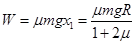
若μ< ,则μmg<qE
,则μmg<qE
小环经过往复运动,最后在P点速度为0,
据动能定理qE·5R-mg·2R-W2=0
克服摩擦力做功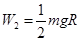
考点:动能定理的应用;带电粒子在匀强电场中的运动

练习册系列答案
相关题目
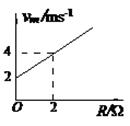
 从距O点为
从距O点为 的P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回。A离开弹簧后,恰好回到P点。物块A与斜面间的动摩擦因数为μ,斜面倾角为
的P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回。A离开弹簧后,恰好回到P点。物块A与斜面间的动摩擦因数为μ,斜面倾角为 。求:
。求:
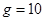 m/s2)
m/s2)
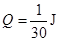 ,试求此过程中外力F对甲做的功.
,试求此过程中外力F对甲做的功.

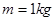 ,半径分别为
,半径分别为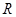 和
和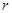 ,两板之间用一根长
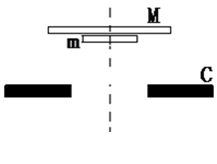
,两板之间用一根长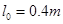 的轻绳将薄板中心相连结(未画出).开始时,两板水平放置并叠合在一起,静止于距离固定支架C高度
的轻绳将薄板中心相连结(未画出).开始时,两板水平放置并叠合在一起,静止于距离固定支架C高度 处. 然后自由下落到C上,支架上有一半径为
处. 然后自由下落到C上,支架上有一半径为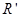 (
(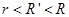 )的圆孔,圆孔与两薄板中心均在圆板中心轴线上. 薄板M与支架发生没有机械能损失的碰撞(碰撞时间极短). 碰撞后,两板即分离,直到轻绳绷紧.在轻绳绷紧的瞬间,两板立即具有共同速度.不计空气阻力,
)的圆孔,圆孔与两薄板中心均在圆板中心轴线上. 薄板M与支架发生没有机械能损失的碰撞(碰撞时间极短). 碰撞后,两板即分离,直到轻绳绷紧.在轻绳绷紧的瞬间,两板立即具有共同速度.不计空气阻力,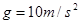 ,求:
,求: