题目内容
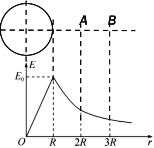
【题目】如图所示，LMN是竖直平面内固定的光滑绝缘轨道，MN水平且足够长，LM下端与MN相切。质量为m的带正电小球B静止在水平轨道上，质量为2m的带正电小球A从上距水平轨道高为h处由静止释放。在A球进入水平轨道之前，由于A、B两球相距足够远，相互作用的静电力忽略不计，A、B两球组成的系统的电势能可认为是零，带电小球均可视为质点。己知重力加速度为g。
(1)A、B两球相距最近时，求A球的速度大小v.
(2)A、B两球相距最近时，求A、B两球组成的系统的电势能EP
(3)求A、B两球最终的速度大小vA、vB
【答案】（1）
（2）
mgh（3）
；
【解析】
(1)对
球下滑的过程，由动能定理得：
解得：
(2)当球进入水平轨道后，、
两球组成的系统动量守恒，当、相距最近时，两球速度相等，由动量守恒定律可得：
由能量守恒定律得：
联立解得：
(3)当、相距最近之后，由于静电斥力的相互作用，它们将会相互远离，当它们相距足够远时，它们之间的相互作用力可视为零，电势能也视为零，它们就达到最终的速度，该过程中，、两球组成的系统动量守恒、能量也守恒，由动量守恒定律可得：
由能量守恒定律可得：
解得：
练习册系列答案
相关题目
