题目内容
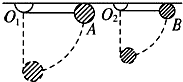
 如图所示,两质量相同的小球A、B,分别用细线悬挂于等高的两点,A球的悬线比B球的长,把两球均拉到悬线水平后将小球由静止释放,以悬点所在平面为参考平面,则两球经最低点时( )
如图所示,两质量相同的小球A、B,分别用细线悬挂于等高的两点,A球的悬线比B球的长,把两球均拉到悬线水平后将小球由静止释放,以悬点所在平面为参考平面,则两球经最低点时( )分析:A、B两球在运动的过程中,只有重力做功,机械能守恒,比较出初始位置的机械能即可知道在最低点的机械能大小.
根据动能定理mgL=
mv2,可比较出A、B两球的速度大小.
根据动能定理或机械能守恒求出在最低点的速度,然后根据F-mg=m
,得出拉力的大小,从而可以比较出两球摆线的拉力.
根据动能定理mgL=
| 1 |
| 2 |
根据动能定理或机械能守恒求出在最低点的速度,然后根据F-mg=m
| v2 |
| L |
解答:解:A、根据动能定理mgL=
mv2,得:v=
,所以A球的速度大于B球的速度,故A错误.
B、根据动能的表达式EK=
mv2,得:A球的动能大于B球的动能,故B错误.
C、A、B两球在运动的过程中,只有重力做功,机械能守恒,初始位置的机械能相等,所以在最低点,两球的机械能相等.故C正确.
D、在最低点,根据牛顿第二定律得:
F-mg=m
,
得F=mg+m
=3mg,与绳的长度无关.所以两绳拉力大小相等.故D正确.
故选CD
| 1 |
| 2 |
| 2gL |
B、根据动能的表达式EK=
| 1 |
| 2 |
C、A、B两球在运动的过程中,只有重力做功,机械能守恒,初始位置的机械能相等,所以在最低点,两球的机械能相等.故C正确.
D、在最低点,根据牛顿第二定律得:
F-mg=m
| v2 |
| L |
得F=mg+m
| v2 |
| L |
故选CD
点评:解决本题的关键掌握动能定理和机械能守恒定律,知道摆球在最低点靠合力提供做圆周运动的向心力.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
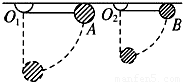
 如图所示,两质量相同的小球A、B,分别用线悬在等高的O1、O2点,A球的悬线比B球的悬线长,把两球的悬线均拉到水平后将小球无初速释放,以悬点为零势能参考面,经过最低点时A球的动能EkA、A球的机械能EA,B球的动能EkB、B球的机械能EB,则EkA
如图所示,两质量相同的小球A、B,分别用线悬在等高的O1、O2点,A球的悬线比B球的悬线长,把两球的悬线均拉到水平后将小球无初速释放,以悬点为零势能参考面,经过最低点时A球的动能EkA、A球的机械能EA,B球的动能EkB、B球的机械能EB,则EkA