题目内容
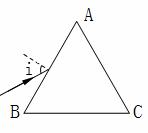
 研究发光物体的光谱通常需要三棱镜,如图所示是截面为等边三角形ABC的三棱镜,一束光从AB边的P点射入棱镜,当入射角i=60°时,进入棱镜的折射光线与BC边平行.求:
研究发光物体的光谱通常需要三棱镜,如图所示是截面为等边三角形ABC的三棱镜,一束光从AB边的P点射入棱镜,当入射角i=60°时,进入棱镜的折射光线与BC边平行.求:①光在棱镜中的传播速度v(光在真空中传播速度c=3×108m/s);
②入射光经过棱镜两次折射后偏转的角度θ.
分析:①作出光路图,由几何知识确定出折射角,即可由折射定律求折射率n,得到光在棱镜中的传播速度v=
.
②根据光路的可逆性原理和几何关系得到入射光经过棱镜两次折射后偏转的角度θ.
| c |
| n |
②根据光路的可逆性原理和几何关系得到入射光经过棱镜两次折射后偏转的角度θ.
解答:解:①由几何知识得:第一次折射时折射角为r=30°.
由折射定律得:折射率 n=

解得 n=
则 光在棱镜中的传播速度 v=
=1.73×108m/s
②由几何关系可知:偏转角 θ=2(i-r)=2×(60°-30°)=60°
答:①光在棱镜中的传播速度v是1.73×108m/s;
②入射光经过棱镜两次折射后偏转的角度θ是60°.
由折射定律得:折射率 n=
| sini |
| sinr |

解得 n=
| 3 |
则 光在棱镜中的传播速度 v=
| c |
| n |
②由几何关系可知:偏转角 θ=2(i-r)=2×(60°-30°)=60°
答:①光在棱镜中的传播速度v是1.73×108m/s;
②入射光经过棱镜两次折射后偏转的角度θ是60°.
点评:本题是简单的几何光学问题,关键要正确作出光路图,运用折射定律、光速公式和几何知识结合进行研究.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目