题目内容
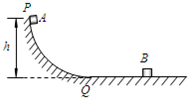 (2010?西城区一模)如图所示,竖直平面内的光滑弧形轨道的底端恰好与光滑水平面相切.质量为M=2.0kg的小物块B静止在水平面上.质量为m=1.0kg的小物块A从距离水平面高h=0.45m的P点沿轨道从静止开始下滑,经过弧形轨道的最低点Q滑上水平面与B相碰,碰后两个物体以共同速度运动.取重力加速度g=10m/s2.求
(2010?西城区一模)如图所示,竖直平面内的光滑弧形轨道的底端恰好与光滑水平面相切.质量为M=2.0kg的小物块B静止在水平面上.质量为m=1.0kg的小物块A从距离水平面高h=0.45m的P点沿轨道从静止开始下滑,经过弧形轨道的最低点Q滑上水平面与B相碰,碰后两个物体以共同速度运动.取重力加速度g=10m/s2.求(1)A经过Q点时速度的大小v0;
(2)A与B碰后速度的大小v;
(3)碰撞过程中系统(A、B)损失的机械能△E.
分析:(1)滑块从P到Q过程中应用动能定理可以求出滑块的速度.
(2)A、B系统动量守恒,由动量守恒定律可以求出两滑块碰后的速度.
(3)系统动能的变化量等于系统损失的机械能.
(2)A、B系统动量守恒,由动量守恒定律可以求出两滑块碰后的速度.
(3)系统动能的变化量等于系统损失的机械能.
解答:解:(1)从P到Q过程,由动能定理可得:
mgh=
mv02-0,解得v0=3m/s;
(2)碰撞过程中,A、B动量守恒,
由动量守恒定律得:mAv0=(mA+mB)v,
解得:v=1m/s;
(3)碰撞过程中,由能量守恒定律得:
△E=
mAv02-=
(mA+mB)v2=3J;
答:(1)A经过Q点时速度的大小3m/s;
(2)A与B碰后速度的大小1m/s;
(3)碰撞过程中系统(A、B)损失的机械能为3J.
mgh=
| 1 |
| 2 |
(2)碰撞过程中,A、B动量守恒,
由动量守恒定律得:mAv0=(mA+mB)v,
解得:v=1m/s;
(3)碰撞过程中,由能量守恒定律得:
△E=
| 1 |
| 2 |
| 1 |
| 2 |
答:(1)A经过Q点时速度的大小3m/s;
(2)A与B碰后速度的大小1m/s;
(3)碰撞过程中系统(A、B)损失的机械能为3J.
点评:本题难度不大,熟练应用动能定理、动量守恒定律与能量守恒定律即可正确解题;第一问也可以应用机械能守恒定律解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
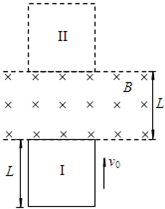 (2010?西城区一模)如图所示,空间存在一有边界的条形匀强磁场区域,磁场方向与竖直平面(纸面)垂直,磁场边界的间距为L.一个质量为m、边长也为L的正方形导线框沿竖直方向运动,线框所在平面始终与磁场方向垂直,且线框上、下边始终与磁场的边界平行.t=0时刻导线框的上边恰好与磁场的下边界重合(图中位置I),导线框的速度为v0.经历一段时间后,当导线框的下边恰好与磁场的上边界重合时(图中位置II),导线框的速度刚好为零.此后,导线框下落,经过一段时间回到初始位置I.则( )
(2010?西城区一模)如图所示,空间存在一有边界的条形匀强磁场区域,磁场方向与竖直平面(纸面)垂直,磁场边界的间距为L.一个质量为m、边长也为L的正方形导线框沿竖直方向运动,线框所在平面始终与磁场方向垂直,且线框上、下边始终与磁场的边界平行.t=0时刻导线框的上边恰好与磁场的下边界重合(图中位置I),导线框的速度为v0.经历一段时间后,当导线框的下边恰好与磁场的上边界重合时(图中位置II),导线框的速度刚好为零.此后,导线框下落,经过一段时间回到初始位置I.则( )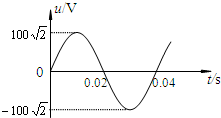 (2010?西城区一模)一理想变压器原、副线圈匝数比n1:n2=5:3.原线圈两端接一正弦式交变电流,其电压u随时间t变化的规律如图所示.当副线圈仅接入一个100Ω的纯电阻用电器时,用电器恰能正常工作.则( )
(2010?西城区一模)一理想变压器原、副线圈匝数比n1:n2=5:3.原线圈两端接一正弦式交变电流,其电压u随时间t变化的规律如图所示.当副线圈仅接入一个100Ω的纯电阻用电器时,用电器恰能正常工作.则( )