Question

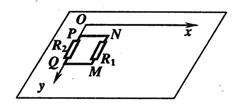
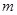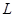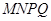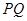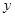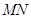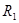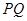(16分)如图所示，空间存在一个方向垂直桌面向下的磁场。现将质量为、边长为的正方形线框，静止放在光滑绝缘足够大的水平桌面上，边与轴重合。边的电阻为，边的电阻为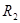，线框其余部分电阻不计。

(1)若磁场随时间的变化规律为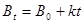 (为大于零的已知常数)，求线框中感应电流的大小和方向。

(2)若磁场不随时间变化，而是按照下列情况分布：磁感应强度沿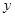轴方向均匀分布，沿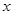轴方向按规律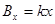变化(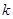为大于零的已知常数)，线框从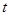=0时刻、以初速度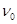由图示位置向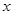轴正方向平动。求在图示位置线框所受安培力的大小和方向。

(3)在第(2)问中，若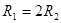，求在整个运动过程中，电阻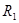产生的焦耳热。

 

Answer 1

【答案】

（1） 感应电流的大小   ，感应电流的方向沿NPQMN。                               （2）安培力大小为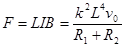，安培力方向沿－x方向（或水平向左）                         （3）电阻R₁产生的焦耳热为

【解析】

试题分析：（1）根据法拉第电磁感应定律可知:

                   

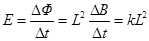
感应电流的大小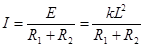         

感应电流的方向沿NPQMN。                             

(2）MN处的磁感应强度为kL，所以MN切割产生的电动势E=BLv₀=kL²v₀，

PQ处磁感应强度为0，所以其产生的电动势也为0，              

因此线框中的感应电动势E= kL²v₀                                             

线框中的感应电流                      

线框受的安培力方向沿－x方向（或水平向左）                

安培力大小为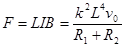                               

（3）线框最终停止，根据能量关系，线框中产生的焦耳热为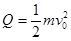 

电阻R₁产生的焦耳热为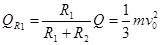          

考点：法拉第电磁感应定律；楞次定律．焦耳定律。

点评：准确理解和应用法拉第电磁感应定律求感应电动势的大小，应用楞次定律判断感应电流的方向是电磁感应的基本内容。