题目内容
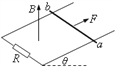
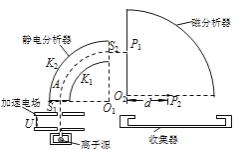
【题目】如图为某种质谱仪的结构的截面示意图,该种质谱仪由加速电场、静电分析器、磁分析器及收集器组成。其中静电分析器由两个相互绝缘且同心的四分之一圆柱面的金属电极K1和K2构成,两柱面电极的半径分别为R1和R2,O1点是圆柱面电极的圆心。S1和S2分别为静电分析器两端为带电粒子进出所留的狭缝。静电分析器中的电场的等势面在该截面图中是一系列以O1为圆心的同心圆弧,图中虚线A是到K1、K2距离相等的等势线。磁分析器中有以O2为圆心的四分之一圆弧的区域,该区域有垂直于截面的匀强磁场,磁场左边界与静电分析器的右边界平行。P1为磁分析器上为带电粒子进入所留的狭缝,O2P1的连线与O1S1的连线垂直。
离子源不断地发出正离子束,正离子束包含电荷量均为q的两种质量分别为m、m′(m<m′<2m)的同位素离子,其中质量为m的同位素离子个数所占的百分比为α。离子束从离子源发出的初速度可忽略不计,经电压为U的加速电场加速后,全部从狭缝S1沿垂直于O1S1的方向进入静电分析器。稳定情况下,离子束进入静电分析器时的等效电流为I。进入静电分析器后,质量为m的同位素离子沿等势线A运动并从狭缝S2射出静电分析器,而后由狭缝P1沿垂直于O2P1的方向进入磁场中,偏转后从磁场下边界中点P2沿垂直于O2P2的方向射出,最后进入收集器。忽略离子的重力、离子之间的相互作用、离子对场的影响和场的边缘效应。
(1)求静电分析器中等势线A上各点的电场强度E的大小;
(2)通过计算说明质量为m′的同位素离子能否从狭缝S2射出电场并最终从磁场下边界射出;
(3)求收集器单位时间内收集的离子的质量M0
【答案】(1)![]() (2)能从磁场下边界射出(3)
(2)能从磁场下边界射出(3) ![]()
【解析】
根据动能定理求得加速后获得的速度,根据运动轨迹判断出在静电分析器中的半径,利用电场力提供向心力求得点场强度;根据动能定理求得在加速电场中获得的速度,在磁场中,根据洛伦兹力提供粒子作圆周运动所需的向心力,根据几何关系求得,即可判断;有离子都能进入磁场并从磁场下边界射出进入收集器,由题意可知,进入收集器的离子中,质量为m的离子个数![]() ,质量为m′的离子个数
,质量为m′的离子个数![]() ,即可求得;
,即可求得;
解:(1)由题意可知,等势线A的半径为:![]()
质量为m的离子在静电分析器中做匀速圆周运动,根据牛顿第二定律有:![]()
设质量为m的离子从狭缝S,进入静电分析器时的速度为v,则其在加速电场中加速过程中,根据动能定理有:![]()
解得:![]()
(2)设质量为m′的离子经加速电场加速后,速度为v′,由动能定理可得:![]()
质量为m′的离子在电场中做半径为R的匀速圆周运动,所需要的向心力为:![]() 解得:
解得:![]()
即该离子所受电场力,恰好等于它若做匀速圆周运动的向心力,因此这个离子仍然在静电分析器中做半径为R的匀速圆周运动.故质量为m′的离子能从狭缝S2射出,仍从狭缝P1进入磁场做匀速圆周运动
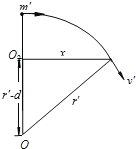
设质量为m′的离子进入磁场做匀速圆周运动的半径为r′,![]() ,若质量为m′的离子能从磁场下边界射出,则出射位置到O2距离为x须满足的条件为
,若质量为m′的离子能从磁场下边界射出,则出射位置到O2距离为x须满足的条件为![]()
质量为m的离子在磁分析器中做匀速圆周运动,根据牛顿第二定律有:![]()
离子在磁分析器中做匀速圆周运动的半径:![]() ,
,![]()
由题意可知,质量为m的离子圆周运动的轨道半径r=d
所以质量为m′的离子在磁分析器中做匀速圆周运动的半径为:![]()
因![]() ,故
,故![]()
则由几何关系有:![]()
解得:![]() ,所以质量为m′的离子能从磁场下边界射出
,所以质量为m′的离子能从磁场下边界射出
(3)时间△t内能进入静电分析器的离子个数:![]()
因所有离子都能进入磁场并从磁场下边界射出进入收集器,由题意可知,进入收集器的离子中,质量为m的离子个数![]() ,质量为m′的离子个数为:
,质量为m′的离子个数为:![]()
解得:![]()

【题目】2008年9月25日至28日我国成功实施了“神舟”七号载入航天飞行并实现了航天员首次出舱。飞船先沿椭圆轨道飞行,后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟。下列判断正确的是( )
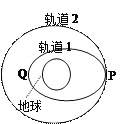
A.飞船变轨前后的机械能相等 |
B.飞船在圆轨道上时航天员出舱前后都处于失重状态 |
C.飞船在此圆轨道上运动的角度速度大于同步卫星运动的角速度 |
D.飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度 |