题目内容
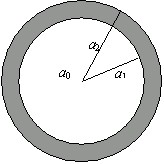
(25分)一个用绝缘材料制成的扁平薄圆环,其内、外半径分别为a1、a2,厚度可以忽略.两个表面都带有电荷,电荷面密度![]() 随离开环心距离r变化的规律均为
随离开环心距离r变化的规律均为![]() ,
,![]() 为已知常量.薄圆环绕通过环心垂直环面的轴以大小不变的角加速度
为已知常量.薄圆环绕通过环心垂直环面的轴以大小不变的角加速度![]() 减速转动,t = 0时刻的角速度为
减速转动,t = 0时刻的角速度为![]() .将一半径为a0 (a0<<a1)、电阻为R并与薄圆环共面的导线圆环与薄圆环同心放置.
.将一半径为a0 (a0<<a1)、电阻为R并与薄圆环共面的导线圆环与薄圆环同心放置.
试求在薄圆环减速运动过程中导线圆环中的张力F与时间t的关系.
提示:半径为r、通有电流I的圆线圈(环形电流),在圆心处产生的磁感应强度为![]() (k为已知常量)
(k为已知常量)
用半径分别为r1(>a1),r2,…,ri,…,rn–1(<a2)的n-1个同心圆把塑料薄圆环分割成n个细圆环.第i个细圆环的宽度为![]() ,其环带面积
,其环带面积
![]()
式中已略去高阶小量![]() .,该细圆环带上、下表面所带电荷量之和为
.,该细圆环带上、下表面所带电荷量之和为
![]()
设时刻t,细圆环转动的角速度为ω ,
![]()
单位时间内,通过它的“横截面”的电荷量,即为电流
![]()
由环形电流产生磁场的规律,该细圆环的电流在环心产生的磁感应强度为
![]() (1)
(1)
式中![]() 是一个微小量,注意到
是一个微小量,注意到![]() ,有
,有
![]() (2)
(2)
将各细圆环产生的磁场叠加,由(1)、(2)式得出环心O点处的磁感应强度:
![]() (3)
(3)
由于a0<<a1,可以认为在导线圆环所在小区域的磁场是匀强磁场,可由O点的场表示.磁场对导线环的磁通量
![]() (4)
(4)
由于![]() 是变化的,所以上述磁通量是随时间变化的,产生的感应电动势的大小为
是变化的,所以上述磁通量是随时间变化的,产生的感应电动势的大小为
![]() (5)
(5)
由全电路欧姆定律可知,导线环内感应电流的大小为
![]() (6)
(6)
设题图中薄圆环带正电作逆时针旋转,穿过导线圆环的磁场方向垂直纸面向外,由于薄圆环环作减角速转动,穿过导线圆环的磁场逐渐减小,根据楞次定律,导线圆环中的感应电流亦为逆时针方向,导线圆环各元段Δl所受的安培力都沿环半径向外.现取对于y轴两对称点U、V,对应的二段电流元![]() 所受的安培力的大小为
所受的安培力的大小为

![]() (7)
(7)
方向如图所示,它沿x及y方向分量分别
![]() (8)
(8)
![]() (9)
(9)
根据对称性,作用于沿半个导线圆环QMN上的各电流元的安培力的x分量之和相互抵消,即
![]() (10)
(10)
(式中![]() ,当
,当![]() 时,
时,![]() 是正的,当
是正的,当![]() 时,
时,![]() 是负的,故
是负的,故![]() ),
),
而作用于沿半个导线圆环QMN上的各电流元的安培力的y分量之和为
![]() (11)
(11)
(式中![]() ,由于θ 在0~π之间
,由于θ 在0~π之间![]() 都是正的,故
都是正的,故![]() ),
),
即半个导线圆环上受的总安培力的大小为![]() ,方向沿y正方向,由于半个圆环处于平衡状态,所以在导线截面Q、N处所受(来自另外半个圆环)的拉力(即张力)F应满足
,方向沿y正方向,由于半个圆环处于平衡状态,所以在导线截面Q、N处所受(来自另外半个圆环)的拉力(即张力)F应满足![]() .由(3)、(6)两式得
.由(3)、(6)两式得
![]() (12)
(12)
由(12)式可见,张力F随时间t线性减小.

 为监测巴河附近一造纸厂的含有离子的污水排放情况,技术人员在排污管中安装了监测装置,该装置的核心部分是一个用绝缘材料制成的空腔,其宽和高分别为b和c,左、右两端开口与排污管相连,如图所示.在垂直于上、下底面方向加磁感应强度大小为B的匀强磁场,在空腔前、后两个侧面上各有长为a的相互平行且正对的电极M和N,M和N与内阻为R的电流表相连.污水从左向右流经该装置时,电流表将显示出污水排放情况.下列说法中正确的是( )
为监测巴河附近一造纸厂的含有离子的污水排放情况,技术人员在排污管中安装了监测装置,该装置的核心部分是一个用绝缘材料制成的空腔,其宽和高分别为b和c,左、右两端开口与排污管相连,如图所示.在垂直于上、下底面方向加磁感应强度大小为B的匀强磁场,在空腔前、后两个侧面上各有长为a的相互平行且正对的电极M和N,M和N与内阻为R的电流表相连.污水从左向右流经该装置时,电流表将显示出污水排放情况.下列说法中正确的是( )| A、M板比N板电势高 | B、污水中离子浓度越高,则电流表的示数越小 | C、污水流量越大,则电流表的示数越大 | D、若只增大所加磁场的磁感应强度,则电流表的示数将减小 |
 (2012?杭州模拟)为监测某化工厂的含有离子的污水排放情况,技术人员在排污管中安装了监测装置,该装置的核心部分是一个用绝缘材料制成的空腔,其宽和高分别为b和c,左、右两端开口与排污管相连,如图所示.在垂直于上、下底面方向加磁感应强度大小为B的匀强磁场,在空腔前、后两个侧面上各有长为a的相互平行且正对的电极M和N,M和N与内阻为R的电流表相连.污水从左向右流经该装置时,电流表将显示出污水排放情况.下列说法中错误的是( )
(2012?杭州模拟)为监测某化工厂的含有离子的污水排放情况,技术人员在排污管中安装了监测装置,该装置的核心部分是一个用绝缘材料制成的空腔,其宽和高分别为b和c,左、右两端开口与排污管相连,如图所示.在垂直于上、下底面方向加磁感应强度大小为B的匀强磁场,在空腔前、后两个侧面上各有长为a的相互平行且正对的电极M和N,M和N与内阻为R的电流表相连.污水从左向右流经该装置时,电流表将显示出污水排放情况.下列说法中错误的是( ) 为监测某化工厂的含有离子的污水排放情况,技术人员在排污管中安装了监测装置,该装置的核心部分是一个用绝缘材料制成的空腔,其宽和高分别为b和c,左、右两端开口与排污管相连,如图所示.在垂直于上、下底面方向加磁感应强度大小为B的匀强磁场,在空腔前、后两个侧面上各有长为a的相互平行且正对的电极M和N,M和N与内阻为R的电流表相连.污水从左向右流经该装置时,电流表将显示出污水排放情况.下列说法中正确的是( )
为监测某化工厂的含有离子的污水排放情况,技术人员在排污管中安装了监测装置,该装置的核心部分是一个用绝缘材料制成的空腔,其宽和高分别为b和c,左、右两端开口与排污管相连,如图所示.在垂直于上、下底面方向加磁感应强度大小为B的匀强磁场,在空腔前、后两个侧面上各有长为a的相互平行且正对的电极M和N,M和N与内阻为R的电流表相连.污水从左向右流经该装置时,电流表将显示出污水排放情况.下列说法中正确的是( ) 、
、 ,厚度可以忽略。两个上下表面都带有电荷,每个面的电荷面密度
,厚度可以忽略。两个上下表面都带有电荷,每个面的电荷面密度 为已知常量。薄圆环绕通过环心垂直环面的轴以
为已知常量。薄圆环绕通过环心垂直环面的轴以 转动。将一半径为
转动。将一半径为
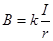 (
( 为已知常量)
为已知常量) 、
、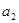 ,厚度可以忽略。两个上下表面都带有电荷,每个面的电荷面密度
,厚度可以忽略。两个上下表面都带有电荷,每个面的电荷面密度 为已知常量。薄圆环绕通过环心垂直环面的轴以
为已知常量。薄圆环绕通过环心垂直环面的轴以 转动。将一半径为
转动。将一半径为
 、电阻为
、电阻为 并与薄圆环共面的导线圆环与薄圆环同心放置。试求:
并与薄圆环共面的导线圆环与薄圆环同心放置。试求:
 减速转动,
减速转动, 时刻的角速度为
时刻的角速度为 ,在薄圆环减速运动过程中导线圆环中的感应电动势为多少?
,在薄圆环减速运动过程中导线圆环中的感应电动势为多少? 、通有电流
、通有电流 的圆线圈(环形电流),在圆心处产生的磁感应强度为
的圆线圈(环形电流),在圆心处产生的磁感应强度为 (
( 为已知常量)
为已知常量)