题目内容
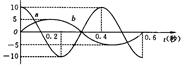
如图所示为水平放置的两个弹簧振子A和B的振动图像,已知两个振子质量之比为mA :mB=2:3,弹簧的劲度系数之比为kA:kB=3:2,则它们的周期之比TA:TB= ;它们的最大加速度之比为aA:aB= 。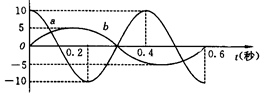
2:3;9:2
解析考点:简谐运动的回复力和能量.
分析:根据弹簧振子的周期公式T="2π"  求两弹簧振子的周期之比.根据简谐运动的特征:F=-kx分析振子加速度达到最大的条件,根据牛顿第二定律求出最大加速度之比.
求两弹簧振子的周期之比.根据简谐运动的特征:F=-kx分析振子加速度达到最大的条件,根据牛顿第二定律求出最大加速度之比.
解:已知两个振子质量之比为mA:mB=2:3,弹簧的劲度系数之比为kA:kB=3:2,根据弹簧振子的周期公式T=2π 得,周期之比TA:TB=
得,周期之比TA:TB= :
: =2:3.根据简谐运动的特征:F=-kx,分析得知,当振子的位移最大时,加速度最大.振子的最大位移大小等于振幅.由图读出,振幅之比AA:AB=2:1.根据牛顿第二定律得最大加速度之比为aA:aB=
=2:3.根据简谐运动的特征:F=-kx,分析得知,当振子的位移最大时,加速度最大.振子的最大位移大小等于振幅.由图读出,振幅之比AA:AB=2:1.根据牛顿第二定律得最大加速度之比为aA:aB= :
: =9:2
=9:2
故答案为:2:3,9:2.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图所示为水平放置的两个弹簧振子A和B的振动图象,已知两个振子质量之比为mA:mB=2:3,弹簧的劲度系数之比为kA:kB=3:2,则它们的周期之比TA:TB=
如图所示为水平放置的两个弹簧振子A和B的振动图象,已知两个振子质量之比为mA:mB=2:3,弹簧的劲度系数之比为kA:kB=3:2,则它们的周期之比TA:TB=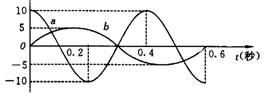
 B=2:3,弹簧的劲度系数之比为kA:kB=3:2,则它们的周期之比TA:TB= ;它们的最大加速度之比为aA:aB= 。
B=2:3,弹簧的劲度系数之比为kA:kB=3:2,则它们的周期之比TA:TB= ;它们的最大加速度之比为aA:aB= 。