题目内容
两块平行金属板MN、PQ水平放置，两板间距为d、板长为l，在紧靠平行板右侧的正三角形区域内存在着垂直纸面的匀强磁场，三角形底边BC与PQ在同一水平线上，顶点A与MN在同一水平线上，如图所示．一个质量为m、电量为+q的粒子沿两板中心线以初速度v0水平射入，若在两板间加某一恒定电压，粒子离开电场后垂直AB边从D点进入磁场，BD=
AB，并垂直AC边射出（不计粒子的重力）．求：
（1）两极板间电压；
（2）三角形区域内磁感应强度；
（3）若两板间不加电压，三角形区域内的磁场方向垂直纸面向外．要使粒子进入磁场区域后能从AB边射出，试求所加磁场的磁感应强度最小值．
| 1 | 4 |
（1）两极板间电压；
（2）三角形区域内磁感应强度；
（3）若两板间不加电压，三角形区域内的磁场方向垂直纸面向外．要使粒子进入磁场区域后能从AB边射出，试求所加磁场的磁感应强度最小值．
分析：（1）根据几何关系，可求速度间的关系，从而即可求解；
（2）由几何关系，结合运动的半径公式，从而可确定磁场的大小，由运动轨迹，结合左手定则可确定磁场的方向；
（3）由粒子刚好与BC边相切时，磁感应强度最小，并根据牛顿第二定律与几何关系，从而即可求解．
（2）由几何关系，结合运动的半径公式，从而可确定磁场的大小，由运动轨迹，结合左手定则可确定磁场的方向；
（3）由粒子刚好与BC边相切时，磁感应强度最小，并根据牛顿第二定律与几何关系，从而即可求解．
解答：解：（1）垂直AB边进入磁场，由几何知识得：粒子离开电场时偏转角为30°
∵vy=
.
tgθ=
∴u=
（2）由几何关系得：lAB=
在磁场中运动半径r1=
lAB=
d
∴B1qv =
v=
∴B1=
方向垂直纸面向里
（3）当粒子刚好与BC边相切时，磁感应强度最小，
由几何知识知粒子的运动半径r2为：r2=
B2qv0=
∴B2=
即：磁感应强度的最小值为
答：（1）两极板间电压u=
；
（2）三角形区域内磁感应强度B1=
；
（3）若两板间不加电压，三角形区域内的磁场方向垂直纸面向外．要使粒子进入磁场区域后能从AB边射出，则所加磁场的磁感应强度最小值为
．
∵vy=
| qu |
| md |
| l |
| v0 |
tgθ=
| vy |
| v0 |
∴u=
| ||||
| 3ql |
（2）由几何关系得：lAB=
| d |
| cos300 |
在磁场中运动半径r1=
| 3 |
| 4 |
| ||
| 2 |
∴B1qv =
m
| ||
| r1 |
| v0 |
| cos30° |
∴B1=
| 4mv0 |
| 3qd |
方向垂直纸面向里
（3）当粒子刚好与BC边相切时，磁感应强度最小，
由几何知识知粒子的运动半径r2为：r2=
| d |
| 4 |
B2qv0=
m
| ||
| r2 |
∴B2=
| 4mv0 |
| qd |
即：磁感应强度的最小值为
| 4mv0 |
| qd |
答：（1）两极板间电压u=
| ||||
| 3ql |
（2）三角形区域内磁感应强度B1=
| 4mv0 |
| 3qd |
（3）若两板间不加电压，三角形区域内的磁场方向垂直纸面向外．要使粒子进入磁场区域后能从AB边射出，则所加磁场的磁感应强度最小值为
| 4mv0 |
| qd |
点评：考查粒子在磁场中运动，结合牛顿第二定律与几何关系来综合应用，掌握运动轨迹的半径与周期公式．
练习册系列答案
相关题目
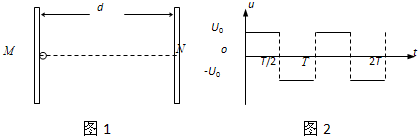
如图所示，两块平行金属板MN间的距离为d，两板间电压u随时间t变化的规律如右图所示电压的绝对值为U0．t=0时刻M板的电势比N板低．在t=0时刻有一个电子从M板处无初速释放，经过1.5个周期刚好到达N板．电子的电荷量为e，质量为m．求：
如图所示，两块平行金属板MN、PQ竖直放置，两板间的电势差U=1.6×103 V，现将一质量m=3.0×10-2 kg、电荷量q=+4.0×10-5 C的带电小球从两板左上方的A点以初速度v0=4.0m/s水平抛出，已知A点距两板上端的高度h=0.45m，之后小球恰好从MN板上端内侧M点进入两板间匀强电场，然后沿直线运动到PQ板上的C点，不计空气阻力，取g=10m/s2，求：