题目内容
(2007?扬州模拟)美国“罗斯福”号核动力航空母舰的动力来自核反应堆,其中主要的核反应方程是
n+
U→
Ba+
Kr+
n
求:
(1)在扩号内填出
n前的系数.
(2)用m1、m2、m3分别表示
U、
Ba、
Kr的质量,m表示中子的质量,则上述核反应方程中一个铀235核发生裂变产生的核能△E是多少?
(3)假设核反应堆的总功率P=6.0×105kW若一个铀235核裂变产生的能量为2.8×10-11J,则该航空母舰在海上航行一个月需要消耗多少千克铀235?( 铀235的摩尔质量m=0.235kg/mol,一个月约为t=2.6×106s,阿伏加德罗常数NA=6.0×1023mol-1,计算结果保留两位有效数字).
1 0 |
235 92 |
141 56 |
92 36 |
1 0 |
求:
(1)在扩号内填出
1 0 |
(2)用m1、m2、m3分别表示
235 92 |
141 56 |
92 36 |
(3)假设核反应堆的总功率P=6.0×105kW若一个铀235核裂变产生的能量为2.8×10-11J,则该航空母舰在海上航行一个月需要消耗多少千克铀235?( 铀235的摩尔质量m=0.235kg/mol,一个月约为t=2.6×106s,阿伏加德罗常数NA=6.0×1023mol-1,计算结果保留两位有效数字).
分析:(1)根据质量数与核电荷数守恒求出系数.
(2)先求出质量亏损,然后由质能方程求出产生的核能.
(3)根据核反应释放的能量与核潜艇需要的能量求出铀的质量.
(2)先求出质量亏损,然后由质能方程求出产生的核能.
(3)根据核反应释放的能量与核潜艇需要的能量求出铀的质量.
解答:解:(1)由质量数与核电荷数守恒可知,产生的中子数为3;
(2)由题意知,质量亏损为△m=m1-m2-m3-2m,由质能方程可知,释放的核能为△E=△mc2=( m1-m2-m3-2m)c2;
(3)一个月核反应产生的总能量为E=Pt,
能量E=
NA△E,则Pt=
NA△E,
解得:m=
=
kg=22kg.
答:(1)
n前的系数为3;
(2)一个铀235核发生裂变产生的核能为(m1-m2-m3-2m)c2;
(3)航空母舰在海上航行一个月需要消耗22千克铀235.
(2)由题意知,质量亏损为△m=m1-m2-m3-2m,由质能方程可知,释放的核能为△E=△mc2=( m1-m2-m3-2m)c2;
(3)一个月核反应产生的总能量为E=Pt,
能量E=
| m |
| μ |
| m |
| μ |
解得:m=
| Ptμ |
| NA△E |
| 6.0×108×2.6×106×0.235 |
| 6.0×1023×2.8×10-11 |
答:(1)
1 0 |
(2)一个铀235核发生裂变产生的核能为(m1-m2-m3-2m)c2;
(3)航空母舰在海上航行一个月需要消耗22千克铀235.
点评:核反应过程中质量数与核电荷数守恒,应用质量数与核电荷数守恒、应用智能方程即可正确解题.

练习册系列答案
相关题目
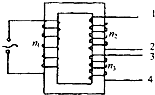 (2007?扬州模拟)如图所示,一个有两个不同副线圈的理想变压器,原线圈匝数为nl=1100匝,两剐线圈的匝 数分别为n2=20匝和n3=70匝.原线圈接入220V交变电压,今将一额定电压为1OV的用电器接入变压器的副线圈输出端后能正常工作,则两个副线圈连接方式应是( )
(2007?扬州模拟)如图所示,一个有两个不同副线圈的理想变压器,原线圈匝数为nl=1100匝,两剐线圈的匝 数分别为n2=20匝和n3=70匝.原线圈接入220V交变电压,今将一额定电压为1OV的用电器接入变压器的副线圈输出端后能正常工作,则两个副线圈连接方式应是( ) (2007?扬州模拟)如图甲所示,带电粒子(不计重力)以水平向右的初速度v0先通过有界匀强电场E,后通过有界匀强磁场B,再从磁场右边穿出,此过程中该粒子动能的改变量为E1;若如图乙所示,将该匀强电场和匀强磁场区域正交叠加,再让该粒子以同样的初速度水平向右穿越叠加场区而从右边穿出,此过程中该粒子动能的改变量为E2.比较场强的大小,下列说法中正确的是( )
(2007?扬州模拟)如图甲所示,带电粒子(不计重力)以水平向右的初速度v0先通过有界匀强电场E,后通过有界匀强磁场B,再从磁场右边穿出,此过程中该粒子动能的改变量为E1;若如图乙所示,将该匀强电场和匀强磁场区域正交叠加,再让该粒子以同样的初速度水平向右穿越叠加场区而从右边穿出,此过程中该粒子动能的改变量为E2.比较场强的大小,下列说法中正确的是( )