题目内容
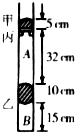 (2013?普陀区二模)一端封闭的粗细均匀的玻璃管,开口向上竖直放置,管内有甲、乙两段水银柱封闭的A、B两部分气体,水银柱甲的底部是一只很薄的活塞丙(活塞重力不计),活塞被管内壁上的小突起物支持着,只能无摩擦地向上运动.已知大气压强为75cmHg,且A中气体压强也是75cmHg,两段空气柱温度都是127℃,其余尺寸如图所示.现保持A中气体温度不变,而使B中气体温度升高.当水银柱甲开始向上移动时,B中气体温度升高了( )
(2013?普陀区二模)一端封闭的粗细均匀的玻璃管,开口向上竖直放置,管内有甲、乙两段水银柱封闭的A、B两部分气体,水银柱甲的底部是一只很薄的活塞丙(活塞重力不计),活塞被管内壁上的小突起物支持着,只能无摩擦地向上运动.已知大气压强为75cmHg,且A中气体压强也是75cmHg,两段空气柱温度都是127℃,其余尺寸如图所示.现保持A中气体温度不变,而使B中气体温度升高.当水银柱甲开始向上移动时,B中气体温度升高了( )分析:A中气体发生等温变化,当水银柱甲开始向上移动时,A的压强等于大气压与上部分水银压强之和,根据玻意耳定律求出此时A气柱的长度,从而得到B气柱的长度和压强,而B气体三个参量都发生改变,由理想气体状态方程求出B中气体的温度,即可得解.
解答:解:对A气体:初态:压强pA=75cmHg,lA=32cm,末态:压强pA′=(75+5)cmHg=80cmHg,长度lA′=?
A气体发生等温变化,由玻意耳定律得
pAlAS=pA′lA′S,
代入解得,lA′=30cm
对B气体:压强pB=(75+10)cmHg=85cmHg,lB=15cm,温度TB=127+273=400K,
末态:压强pB′=(75+10+5)cmHg=90cmHg,长度lB′=(32+15-30)cm=17cm,温度TB′=?
由理想气体状态方程得
=
代入解得,TB′=480K,则温度升高了△TB=TB′-TB=80K
故选A
A气体发生等温变化,由玻意耳定律得
pAlAS=pA′lA′S,
代入解得,lA′=30cm
对B气体:压强pB=(75+10)cmHg=85cmHg,lB=15cm,温度TB=127+273=400K,
末态:压强pB′=(75+10+5)cmHg=90cmHg,长度lB′=(32+15-30)cm=17cm,温度TB′=?
由理想气体状态方程得
| pBlBS |
| TB |
| pB′lB′S |
| TB′ |
代入解得,TB′=480K,则温度升高了△TB=TB′-TB=80K
故选A
点评:本题采用隔离法研究两部分气体的同时,关键是找出它们之间的关系,如气体关系、压强关系.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 (2013?普陀区二模)如图所示为P、Q两物体沿同一直线作直线运动的s-t图,下列说法中正确的有( )
(2013?普陀区二模)如图所示为P、Q两物体沿同一直线作直线运动的s-t图,下列说法中正确的有( ) (2013?普陀区二模)如图所示,斜面与水平面间的夹角θ=37°,物体A和B的质量分别为mA=10kg、mB=5kg.A、B间用质量不计的细绳相连.试求:
(2013?普陀区二模)如图所示,斜面与水平面间的夹角θ=37°,物体A和B的质量分别为mA=10kg、mB=5kg.A、B间用质量不计的细绳相连.试求: