题目内容
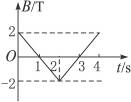
 一个面积S=4×10-2m2、匝数n=100匝的线圈,放在匀强磁场中,磁场方向垂直平面,磁感应强度的大小随时间变化规律如图,由图可知( )
一个面积S=4×10-2m2、匝数n=100匝的线圈,放在匀强磁场中,磁场方向垂直平面,磁感应强度的大小随时间变化规律如图,由图可知( )分析:由图象看出,磁感应强度随时间均匀增大,线圈产生感应电流,由楞次定律判断线圈中感应电流的方向.由法拉第电磁感应定律求出线圈中产生的感应电动势,再由欧姆定律求出感应电流的大小.
解答:解:AB、由图象的斜率求出:
=
T/s=2T/s
因此有:
=
S=2×4×10-2 Wb/s=8×10-2Wb/s,故A正确,B错误;
C、根据法拉第电磁感应定律得:
E=n
=n
S=100×2×4×10-2 V=8V,故C正确;
D、由图看出,结合C选项可知,第3秒末感应电动势仍为8V,故D错误;
故选:AC.
| △B |
| △t |
| 2 |
| 1 |
因此有:
| △? |
| △t |
| △B |
| △t |
C、根据法拉第电磁感应定律得:
E=n
| △? |
| △t |
| △B |
| △t |
D、由图看出,结合C选项可知,第3秒末感应电动势仍为8V,故D错误;
故选:AC.
点评:本题中磁感应强度均匀增大,穿过线圈的磁通量均匀增加,线圈中产生恒定电流,由法拉第电磁感应定律求出感应电动势,再求解感应电流,是经常采用的方法和思路.

练习册系列答案
相关题目
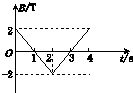 一个面积S=4×10-2 m2、匝数n=100匝的线圈放在匀强磁场中,磁场方向垂直于线圈平面,磁感应强度B随时间t变化的规律如图所示,则下列判断正确的是( )
一个面积S=4×10-2 m2、匝数n=100匝的线圈放在匀强磁场中,磁场方向垂直于线圈平面,磁感应强度B随时间t变化的规律如图所示,则下列判断正确的是( )| A、在开始的2s内穿过线圈的磁通量变化率等于8Wb/s | B、在开始的2s内穿过线圈的磁通量的变化量等于零 | C、在开始的2s内线圈中产生的感应电动势等于8V | D、在第3s末线圈中的感应电动势等于零 |
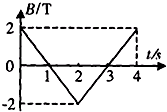 一个面积S=4×10-2m2的闭合线圈,放在匀强磁场中,磁场方向垂直线圈平面,磁场的磁感应强度B的大小随时间的变化规律如图所示( )
一个面积S=4×10-2m2的闭合线圈,放在匀强磁场中,磁场方向垂直线圈平面,磁场的磁感应强度B的大小随时间的变化规律如图所示( )