题目内容
如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以v=5m/s的速度在水平面上向右运动.求小球从A点运动到地面所需的时间(平面与斜面均光滑.g取10m/s2).某同学对此题的解法为:小球沿斜面运动,则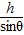 =vt+
=vt+ g sin θ t2,由此可求得落地的时间t.
g sin θ t2,由此可求得落地的时间t.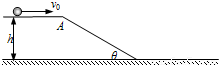
【答案】分析:对物体受力分析可知,物体做平抛运动,研究平抛运动的方法是把平抛运动分解到水平方向和竖直方向去研究,水平方向做匀速直线运动,竖直方向做自由落体运动,两个方向上运动的时间相同.
解答:解:不同意上述解法,小球应在A点离开平面做平抛运动,而不是沿斜面下滑.正确的解法是:
假如小球直接落至地面,则小球在空中运动的时间为
t=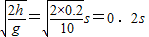
落地点与A点的水平距离x=vt=5×0.2m=1m.
斜面底宽l=hcotθ=0.2×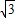 m≈0.35m.
m≈0.35m.
因为x>l,所以小球离开A点后确实不会落到斜面上,而是直接落至地面,因此落地时间即为平抛运动时间0.2s.
答:落地的时间为0.2s
点评:本题就是对平抛运动规律的考查,平抛运动可以分解为在水平方向上的匀速直线运动,和竖直方向上的自由落体运动来求解.
解答:解:不同意上述解法,小球应在A点离开平面做平抛运动,而不是沿斜面下滑.正确的解法是:
假如小球直接落至地面,则小球在空中运动的时间为
t=
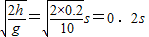
落地点与A点的水平距离x=vt=5×0.2m=1m.
斜面底宽l=hcotθ=0.2×
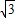 m≈0.35m.
m≈0.35m.因为x>l,所以小球离开A点后确实不会落到斜面上,而是直接落至地面,因此落地时间即为平抛运动时间0.2s.
答:落地的时间为0.2s
点评:本题就是对平抛运动规律的考查,平抛运动可以分解为在水平方向上的匀速直线运动,和竖直方向上的自由落体运动来求解.

练习册系列答案
相关题目
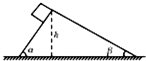 如图所示,一高度为h的楔形物块固定在水平地面上,质量为m的物体由静止开始从倾角分别为α、β的两个光滑斜面的顶端滑下,则下列说法中正确的是( )
如图所示,一高度为h的楔形物块固定在水平地面上,质量为m的物体由静止开始从倾角分别为α、β的两个光滑斜面的顶端滑下,则下列说法中正确的是( )| A、物体滑到斜面底端的速度相同 | B、物体滑到斜面底端所用的时间相同 | C、物体滑到斜面底端时重力所做功的功率相同 | D、物体滑到斜面底端过程中重力所做的功相同 |
 如图所示,一高度为h=0.8m粗糙的水平面在B点处与一倾角为θ=30°光滑的斜面BC连接,一小滑块从水平面上的A点以v0=3m/s的速度在粗糙的水平面上向右运动.运动到B点时小滑块恰能沿光滑斜面下滑.已知AB间的距离s=5m,求:
如图所示,一高度为h=0.8m粗糙的水平面在B点处与一倾角为θ=30°光滑的斜面BC连接,一小滑块从水平面上的A点以v0=3m/s的速度在粗糙的水平面上向右运动.运动到B点时小滑块恰能沿光滑斜面下滑.已知AB间的距离s=5m,求: (2003?上海)如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以v0=5m/s的速度在平面上向右运动.求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2).某同学对此题的解法为:小球沿斜面运动,则
(2003?上海)如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以v0=5m/s的速度在平面上向右运动.求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2).某同学对此题的解法为:小球沿斜面运动,则 如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以v0=5m/s的速度在平面上向右运动,求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2).
如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以v0=5m/s的速度在平面上向右运动,求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2). (2011?皇姑区一模)如图所示,一高度为h的光滑水平面与一倾角为θ的斜面在P点连接,该斜面在Q点处与地面连接.一小球以速度v在光滑水平面上向右运动.则小球经过P点后一段时间内( )
(2011?皇姑区一模)如图所示,一高度为h的光滑水平面与一倾角为θ的斜面在P点连接,该斜面在Q点处与地面连接.一小球以速度v在光滑水平面上向右运动.则小球经过P点后一段时间内( )