题目内容
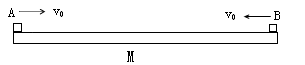
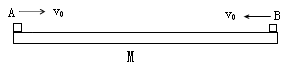
质量为M=0.4kg的平板静止在光滑的水平面上,如图所示,当t=0时,质量为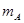 =0.4kg的小物块A和质量为
=0.4kg的小物块A和质量为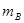 =0.2kg的小物块B,分别从平板左右两端以相同大小的水平速度
=0.2kg的小物块B,分别从平板左右两端以相同大小的水平速度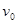 =6.0m/s同时冲上平板,当它们相对于平板都停止滑动时,没有相碰。已知A.B两物块与平板的动摩擦因数都是0.2,g取10m/s2,求:
=6.0m/s同时冲上平板,当它们相对于平板都停止滑动时,没有相碰。已知A.B两物块与平板的动摩擦因数都是0.2,g取10m/s2,求:
(1)A.B两物体在平板上都停止滑动时平板的速度;
(2)从A.B两物块滑上平板到物块A刚相对于平板静止过程中,A.B及平板组成的系统机械能损失;
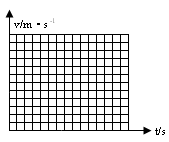
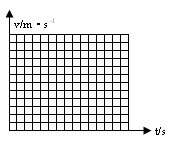
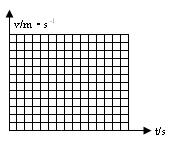
(3)请在下面坐标系中画出平板运动的v—t图象(要写出计算过程)。
⑴设物块 A.B相对于平板停止滑动时,平板速度为v,根据动量守恒定律,有:(mA-mB)vo=(M+ mA+ mB) v
所以得: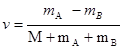 vo
vo
⑵物块A.B滑上平板后各自对地做匀减速运动,且加速度大小相等,因A对平板的摩擦力大于B对平板的摩擦力,故平板向右做匀加速运动。因此,物块A先与平板达到共速,因A.B初速度及加速度大小均相等,故此时B的速度大小与A和平板相等,设为v1 ,根据动量守恒定律得:
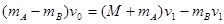
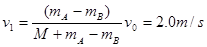
所以,损失机械能为
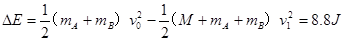
⑶平板的运动分为三个阶段,第一阶段平板做匀加速直线运动至与A达到共速,在此过程所用的时间为t1,对平板运用动量定理,由: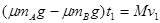 所以t1=2s
所以t1=2s
第二阶段平板与A一起做匀减速直线运动到与B共速,设此过程所用时间为t2,对平板运用动量定理,得: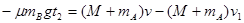 即t2=1.6s
即t2=1.6s
第三阶段平板与AB一起以1.2m/s的速度做匀速直线运动。
故平板的V—t图像如下图所示。

【解析】略


 =0.4kg的小物块A和质量为
=0.4kg的小物块A和质量为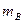 =0.2kg的小物块B,分别从平板左右两端以相同大小的水平速度
=0.2kg的小物块B,分别从平板左右两端以相同大小的水平速度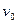 =6.0m/s同时冲上平板,当它们相对于平板都停止滑动时,没有相碰。已知A.B两物块与平板的动摩擦因数都是0.2,g取10m/s2,求:
=6.0m/s同时冲上平板,当它们相对于平板都停止滑动时,没有相碰。已知A.B两物块与平板的动摩擦因数都是0.2,g取10m/s2,求: .B两物块滑上平板到物块A刚相对于平板静止过程中,A.B及平板组成的系统机械能损失;
.B两物块滑上平板到物块A刚相对于平板静止过程中,A.B及平板组成的系统机械能损失;