题目内容
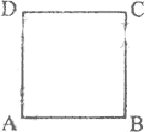 (2009?海南)如图,ABCD是边长为a的正方形.质量为m、电荷量为e的电子以大小为v0的初速度沿纸面垂直于BC变射入正方形区域.在正方形内适当区域中有匀强磁场.电子从BC边上的任意点入射,都只能从A点射出磁场.不计重力,求:
(2009?海南)如图,ABCD是边长为a的正方形.质量为m、电荷量为e的电子以大小为v0的初速度沿纸面垂直于BC变射入正方形区域.在正方形内适当区域中有匀强磁场.电子从BC边上的任意点入射,都只能从A点射出磁场.不计重力,求:(1)此匀强磁场区域中磁感应强度的方向和大小;
(2)此匀强磁场区域的最小面积.
分析:(1)由题意可确定出粒子运动的圆心和半径,则由洛仑兹力及牛顿第二定律可求得磁感应强度B;
(2)由几何关系可得出最小磁场的两个边界,则由几何关系即可求得磁场区域的面积.
(2)由几何关系可得出最小磁场的两个边界,则由几何关系即可求得磁场区域的面积.
解答:解:(1)设匀强磁场的磁感应强度的大小为B.令圆弧
是自C点垂直于BC入射的电子在磁场中的运行轨道.电子所受到的磁场的作用力f=ev0B
应指向圆弧的圆心,因而磁场的方向应垂直于纸面向外.圆弧
的圆心在CB边或其延长线上.依题意,圆心在A、C连线的中垂线上,故B 点即为圆心,圆半径为a按照牛顿定律有f=m
联立①②式得B=
(2)由(1)中决定的磁感应强度的方向和大小,可知自C点垂直于BC入射电子在A点沿DA方向射出,且自BC边上其它点垂直于入射的电子的运动轨道只能在BAEC区域中.因而,圆弧
是所求的最小磁场区域的一个边界.
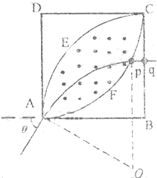
为了决定该磁场区域的另一边界,我们来考察射中A点的电子的速度方向与BA的延长线交角为θ(不妨设0≤θ<
)的情形.该电子的运动轨迹qpA如图所示.
 图中,圆
图中,圆
的圆心为O,pq垂直于BC边,由③式知,圆弧
的半径仍为a,在D为原点、DC为x轴,AD为y轴的坐标系中,P点的坐标(x,y)为x=asinθ
y=-[a-(a-acosθ)]=-acosθ
这意味着,在范围0≤θ≤
内,p点形成以D为圆心、a为半径的四分之一圆周
,它是电子做直线运动和圆周运动的分界线,构成所求磁场区域的另一边界.
因此,所求的最小匀强磁场区域时分别以B和D为圆心、a为半径的两个四分之一圆周
和
所围成的,其面积为S=2(
πa2-
a2)=
a2
 |
| AEC |
应指向圆弧的圆心,因而磁场的方向应垂直于纸面向外.圆弧
 |
| AEC |
| ||
| 2 |
联立①②式得B=
| mv0 |
| ea |
(2)由(1)中决定的磁感应强度的方向和大小,可知自C点垂直于BC入射电子在A点沿DA方向射出,且自BC边上其它点垂直于入射的电子的运动轨道只能在BAEC区域中.因而,圆弧
 |
| AEC |
为了决定该磁场区域的另一边界,我们来考察射中A点的电子的速度方向与BA的延长线交角为θ(不妨设0≤θ<
| π |
| 2 |
 图中,圆
图中,圆 |
| AP |
 |
| AP |
y=-[a-(a-acosθ)]=-acosθ
这意味着,在范围0≤θ≤
| π |
| 2 |
 |
| AFC |
因此,所求的最小匀强磁场区域时分别以B和D为圆心、a为半径的两个四分之一圆周
 |
| AEC |
 |
| AFC |
| 1 |
| 4 |
| 1 |
| 2 |
| π-2 |
| 2 |
点评:在带电粒子在磁场中运动中,要注意圆心及半径的确定;同时应利用好几何关系;此类问题对学生的要求较高,要求学生具有较好的数学功底;在做题时,要注意画图.

练习册系列答案
相关题目
 (2009?海南)两刚性球a和b的质量分别为ma和mb、直径分别为da和db(da>db).将a、b球依次放入一竖直放置平底圆筒内,如图所示.设a、b两球静止时对圆筒侧面的压力大小分别为f1和f2,筒底所受的压力大小为F.已知重力加速度大小为g.若所有接触面都是光滑的,则( )
(2009?海南)两刚性球a和b的质量分别为ma和mb、直径分别为da和db(da>db).将a、b球依次放入一竖直放置平底圆筒内,如图所示.设a、b两球静止时对圆筒侧面的压力大小分别为f1和f2,筒底所受的压力大小为F.已知重力加速度大小为g.若所有接触面都是光滑的,则( ) (2009?海南)一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示.设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合外力从开始至t0时刻做的功是W1,从t0至2t0时刻做的功是W2,则( )
(2009?海南)一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示.设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合外力从开始至t0时刻做的功是W1,从t0至2t0时刻做的功是W2,则( ) (2009?海南)一长直铁芯上绕有一固定线圈M,铁芯右端与一木质圆柱密接,木质圆柱上套有一闭合金属环N,N可在木质圆柱上无摩擦移动.M连接在如图所示的电路中,其中R为滑线变阻器,E1和E2为直流电源,S为单刀双掷开关.下列情况中,可观测到N向左运动的是( )
(2009?海南)一长直铁芯上绕有一固定线圈M,铁芯右端与一木质圆柱密接,木质圆柱上套有一闭合金属环N,N可在木质圆柱上无摩擦移动.M连接在如图所示的电路中,其中R为滑线变阻器,E1和E2为直流电源,S为单刀双掷开关.下列情况中,可观测到N向左运动的是( )