题目内容
【题目】某根水平固定的长滑竿上有n(n≥3)个质量相同的滑扣(即可以滑动的圆环),每相邻的两个滑扣(极薄)之间有不可伸长的柔软轻质细线相连,细线长度均为L,滑扣在滑竿上滑行的阻力大小恒为滑扣对滑竿正压力大小的μ倍。开始时所有滑扣可近似地看成挨在一起(但未相互挤压);今给第1个滑扣一个初速度使其在滑竿上开始向左滑行(平动);在滑扣滑行的过程中,前、后滑扣之间的细线拉紧后都以共同的速度向前滑行,但最后一个(即第n个)滑扣固定在滑竿边缘。已知从第1个滑扣开始的(n一1)个滑扣相互之间都依次拉紧,继续滑行距离l(0<l<L)后静止,且所有细线拉紧过程的时间间隔极短。求:

(1)滑扣1的初速度的大小;
(2)整个过程中克服摩擦力所做的功;
(3)整个过程中仅仅由于细线拉紧引起的总动能损失。
【答案】(1)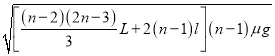 (2)
(2) (3)
(3)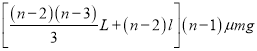
【解析】
(1)为普遍起见,设两个物体质量分别为m1和m2,初速度分别为v1和0,发生完全非弹性碰撞后共同速度为v,则碰前的动能
E=![]() ①
①
由于细绳拉紧前后时间间隔极短,可以忽略摩擦阻力,故前后动量守恒,有
m1v1=(m1+m2)v ②
碰后的动能之和(即系统剩余动能)为
E′=![]() ③
③
由①②③式得
E′=![]() ④
④
此式为后续计算的通式,后续计算特别简单,因为质量相等
损失的动能为
ΔE=E-E′=![]()
设第1个滑扣以速度v10开始运动
E0=![]() ⑤
⑤
在第1个滑扣滑动距离L、第1与第2个滑扣之间的细绳刚拉紧前的瞬间,系统剩余动能为
E1f=E0-μmgL ⑥
在第1个滑扣与第2个滑扣之间的细绳刚拉紧后的瞬前,系统剩余动能为(根据④式)
E20=![]() =
=![]() ⑦
⑦
在第1、2个滑扣共同滑动距离L、第2与第3个滑扣之间的细绳刚拉紧前的瞬间,系统剩余动能为
E2f=E20-2μmgL=![]() =
=![]() ⑧
⑧
在第2个滑扣与第3个滑扣之间的细绳刚拉紧后的瞬前,系统剩余动能为(根据④式)
E30=![]() =
=![]() ⑨
⑨
在第1、2、3个滑扣共同滑动距离L、第3与第4个滑扣之间的细绳刚拉紧前的瞬间,系统剩余动能为 E3f=E30-3μmgL=![]() -3μmgL=
-3μmgL=![]() ⑩
⑩
……
依次类推,在第k个与第k+1个滑扣之间的细绳刚拉紧前的瞬间,系统剩余动能为
Ekf=![]() =
=![]()
=![]() 1≤k≤n-2
1≤k≤n-2
于是,在第(n-2)个与第(n-1)个滑扣之间的细绳刚拉紧前的瞬间,系统剩余动能为
E(n-2)f =![]() ⑾
⑾
在第(n-2)个与第(n-1)个滑扣之间的细绳刚拉紧后的瞬间,系统剩余动能为
E(n-1)0= ![]() =
= ![]() ⑿
⑿
(可类比⑦、⑨,并代入⑾得到)
由⑾知,E(n-2)f >0
![]() >0
>0
E(n-1)f <0
![]() <0,
<0,
得
![]() <E0<
<E0<![]()
本式题目中没有要求的,相当于给出了待求量的定义域
则从第1个滑扣开始的(n-1)个滑扣都依次拉紧,且可继续滑行距离l(0<l<L)后静止。因而有
E(n-1)0= ![]() =(n-1) μmgl (因为要继续滑行距离l) ⒀
=(n-1) μmgl (因为要继续滑行距离l) ⒀
由⑤⒀得滑扣1的初速度的大小
v10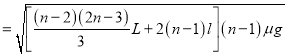
(2)整个过程中克服摩擦力所做的功为
W=μmgL+μ(2m)gL+μ(3m)gL+……+μ[(n-2)m]gL+μ[(n-1)m]gl=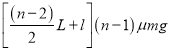
(3)在整个过程中仅仅由于细线拉紧引起的总能量损失为
![]()
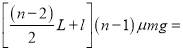
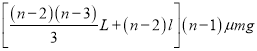

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案