题目内容
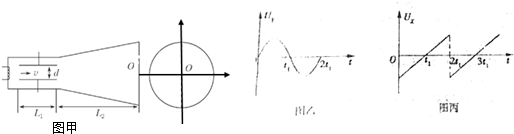
3.某同学利用图甲所示装置,研究物块在桌面上的运动情况.物块在重物的牵引下开始运动,重物落地后,物块再运动一段距离停在桌面上(尚未到达滑轮处).图乙是用图甲所示装置打出的一条纸带.在纸带上按时间顺序选取1,2,3,…,10,11共11个计数点(相邻计数点间还有四个点未画出).测出相邻计数点间的距离,如图乙中数据所示.打点计时器所用电源的频率为50Hz.
(1)只需恰当选取图乙所示纸带的一小段,再查出当地重力加速度g的值,便可求得物块与桌面间的动摩擦因数μ.选取的那一小段纸带应包含D(填选项前的字母代号)计数点.
A.1至6 B.4至8 C.6至11 D.7至11
(2)打计数点“10”时,物块的速度大小为0.56m/s.(保留二位有效数字)
(3)若重力加速度g=10m/s2,则物块与桌面间的动摩擦因数μ=0.18(保留二位有效数字);图甲中重物的质量m与物块质量M之比等于1:2.
分析 (1)由纸带两个点之间的时间相同,若位移逐渐增大,表示物体做加速运动,若位移逐渐减小,则表示物体做减速运动;
(2)用平均速度代替瞬时速度的方法求解瞬时速度;
(3)用作差法求解减速过程中的加速度,再由μ=$\frac{a}{g}$表达式,从而可求出动摩擦因数.
解答 解:(1)从纸带上的数据分析得知:在点计数点6之前,两点之间的位移逐渐增大,是加速运动,在计数点7之后,两点之间的位移逐渐减小,是减速运动,说明物块没有重物的作用,在摩擦阻力作用下,开始做匀减速运动,由纸带数据,可解得加速度,从而求得,动摩擦因数,故D正确,ABC错误;
(2)根据平均速度代替瞬时速度的方法求解瞬时速度,
则有:v10=$\frac{0.066+0.046}{0.2}$m/s=0.56m/s
(3)由纸带可知,计数点7往后做减速运动,根据作差法得:
a=$\frac{0.066+0.046-0.0861-0.106}{0.{2}^{2}}$m/s2=-1.8m/s2.
若用$\frac{a}{g}$来计算物块与木板间的动摩擦因数,则有:μ=$\frac{a}{g}$=$\frac{1.8}{10}$=0.18;
根据加速度公式,求得加速运动的加速度,a′=$\frac{0.09+0.0701-0.0501-0.03}{0.{2}^{2}}$=2.0m/s2
则有:mg-μMg=(M+m)a′
解得:m:M=1:2.
故答案为:(1)D;
(2)0.56;
(3)0.18,1:2.
点评 (1)考查要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用,注意有效数字.
(2)本题主要考察“验证牛顿第二定律”的实验,要明确实验原理,特别是要明确系统误差的来源,知道减小系统误差的方法.

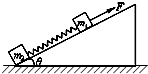 如图所示,质量分别为m1、m2的两个物块间用一轻弹簧连接,放在倾角为θ的粗糙斜面上,物块与斜面间的动摩擦因数均为μ.平行于斜面、大小为F的拉力作用在m1上,使m1、m2一起向上作匀加速运动,斜面始终静止在水平地面上,则( )
如图所示,质量分别为m1、m2的两个物块间用一轻弹簧连接,放在倾角为θ的粗糙斜面上,物块与斜面间的动摩擦因数均为μ.平行于斜面、大小为F的拉力作用在m1上,使m1、m2一起向上作匀加速运动,斜面始终静止在水平地面上,则( )| A. | 弹簧的弹力大小为$\frac{{m}_{2}}{{m}_{1}+{m}_{2}}$F | |
| B. | 弹簧的弹力大小为$\frac{{m}_{2}}{{m}_{1}+{m}_{2}}$F+μm2gcosθ | |
| C. | 地面对斜面的摩擦力一定水平向右 | |
| D. | 地面对斜面的摩擦力可能为零 |
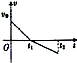
 如图所示,是两列频率相同的水波相遇的某时刻波形图,实线表示的波向右传播,振幅为A1,虚线表示的波向左传播,振幅为A2,介质中有a、b、c三个质点,下列说法正确的是( )
如图所示,是两列频率相同的水波相遇的某时刻波形图,实线表示的波向右传播,振幅为A1,虚线表示的波向左传播,振幅为A2,介质中有a、b、c三个质点,下列说法正确的是( )| A. | a、c点的位移始终为零 | B. | b点的位移可能为零 | ||
| C. | a点以A1+A2的振幅振动 | D. | a、b、c点都以A1-A2的振幅振动 |
| A. | 弹簧秤、细绳、橡皮条都应与木板平行 | |
| B. | 拉橡皮条的细绳要长些,标记同一细绳方向的两点要远些 | |
| C. | 用两弹簧秤同时拉橡皮条时,两弹簧秤示数之差应尽可能大 | |
| D. | 实验中两弹簧秤拉力之间的夹角应取90°,以便于算出合力的大小 |
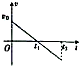
 如图,半径R=0.4m的光滑半圆轨道竖直放置,半圆环与动摩擦因数为μ=0.3的粗糙水平地面相切于圆弧的端点A,一质量m=0.1Kg的小球以初速度v0=7.0m/s在水平地面上向左运动,运动4.0m后冲上圆形轨道.问:
如图,半径R=0.4m的光滑半圆轨道竖直放置,半圆环与动摩擦因数为μ=0.3的粗糙水平地面相切于圆弧的端点A,一质量m=0.1Kg的小球以初速度v0=7.0m/s在水平地面上向左运动,运动4.0m后冲上圆形轨道.问: 如图所示,质量M=8kg的木板放在水平光滑的平面上,在木板左端加一水平拉力F=8N,当木板向右运动的速度达到1.5m/s时,在木板前端轻轻地放上一个大小不计,质量为m=2kg的小物块,物块与木板间的动摩擦因数μ=0.2,木板足够长(取g=10m/s2).求:
如图所示,质量M=8kg的木板放在水平光滑的平面上,在木板左端加一水平拉力F=8N,当木板向右运动的速度达到1.5m/s时,在木板前端轻轻地放上一个大小不计,质量为m=2kg的小物块,物块与木板间的动摩擦因数μ=0.2,木板足够长(取g=10m/s2).求: