【题目】在四棱锥中，平面平面， 底面为梯形, ，.

（Ⅰ）求证：平面；

（Ⅱ）求证：平面；

（Ⅲ）若是棱的中点，求证：对于棱上任意一点，与都不平行

【题目】为迎接年冬奥会，北京市组织中学生开展冰雪运动的培训活动，并在培训结束后对学生进行了考核. 记表示学生的考核成绩，并规定为考核优秀.为了了解本次培训活动的效果，在参加培训的学生中随机抽取了名学生的考核成绩，并作成如下茎叶图：

(Ⅰ)从参加培训的学生中随机选取1人，请根据图中数据，估计这名学生考核成绩为优秀的概率；

(Ⅱ)从图中考核成绩满足的学生中任取人，求至少有一人考核优秀的概率；

(Ⅲ)记表示学生的考核成绩在区间内的概率，根据以往培训数据，规定当时培训有效. 请你根据图中数据，判断此次中学生冰雪培训活动是否有效，并说明理由.

【题目】已知集合，. 若，且对任意，均有，则集合中元素个数的最大值为( )

A. 5 B. 6 C. 11 D. 13

【题目】已知函数（是自然对数的底数）

（1）判断函数极值点的个数，并说明理由；

（2）若， ，求的取值范围.

【题目】如图所示，在正方体中，点是棱上的一个动点，平面交棱于点．给出下列命题：

①存在点，使得//平面；

②对于任意的点，平面平面；

③存在点，使得平面；

④对于任意的点，四棱锥的体积均不变.

其中正确命题的序号是______．（写出所有正确命题的序号）.

A.1B.C.﹣2D.﹣1

【题目】如图，已知多面体的底面是边长为的菱形， 底面， ，且．

（1）证明：平面平面；

（2）若直线与平面所成的角为，求二面角

的余弦值．

（1）求异面直线DC1，B1C所成角的余弦值；

（2）求二面角B1-DC-C1的平面角的余弦值．

【题目】P是圆上的动点，P点在x轴上的射影是D，点M满足．

（1）求动点M的轨迹C的方程，并说明轨迹是什么图形；

（2）过点的直线l与动点M的轨迹C交于不同的两点A，B，求以OA，OB为邻边的平行四边形OAEB的顶点E的轨迹方程．

年级组为了了解学生的体质，随机抽取了100名学生，统计了他的跳绳个数，并绘制了如下样本频率直方图：

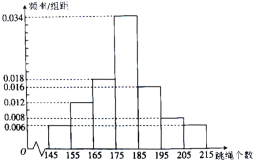
（1）现从这100名学生中，任意抽取2人，求两人得分之和小于35分的概率（结果用最简分数表示）；

（2）若该校高二年级2000名学生，所有学生的一分钟跳绳个数近似服从正态分布，其中，为样本平均数的估计值（同一组中数据以这组数据所在区间的中点值为代表）．利用所得到的正态分布模型解决以下问题：

①估计每分钟跳绳164个以上的人数（四舍五入到整数）

②若在全年级所有学生中随机抽取3人，记每分钟跳绳在179个以上的人数为，求的分布列和数学期望与方差．

（若随机变量服从正态分布则，，）