题目内容
设椭圆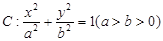 的离心率
的离心率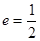 ,右焦点到直线
,右焦点到直线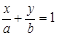 的距离
的距离

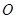 为坐标原点。
为坐标原点。
(I)求椭圆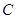 的方程;
的方程;
(II)过点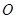 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆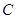 分别交于
分别交于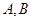 两点,证明点
两点,证明点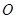 到直
到直
线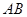 的距离为定值,并求弦
的距离为定值,并求弦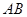 长度的最小值
长度的最小值
【答案】
(I)椭圆C的方程为
(II)弦AB的长度的最小值是
【解析】.解:(I)由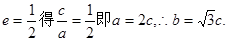
由右焦点到直线 的距离为
的距离为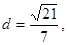
得: 解得
解得
所以椭圆C的方程为 …………4分
…………4分
( II)设
II)设 ,K^S*5U
,K^S*5U
直线AB的方程为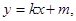
与椭圆 联立消去y得
联立消去y得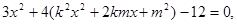

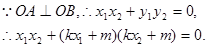
即
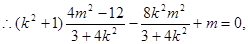
整理得 所以O到直线AB的距离
所以O到直线AB的距离
 …………8分
…………8分
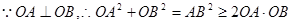 , 当且仅当OA=OB时取“=”号。
, 当且仅当OA=OB时取“=”号。
由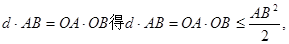

即弦AB的长度的最小值是 …………13分
…………13分

练习册系列答案
相关题目




 的离心率e=
的离心率e= ,左右两个焦分别为F1,F2.过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点,且|MN|=2.
,左右两个焦分别为F1,F2.过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点,且|MN|=2.