题目内容
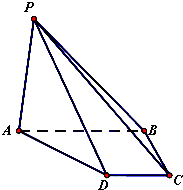 四棱锥P-ABCD的底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=2BC=2CD=2,PA=PD,PA⊥PD,PB=PC.
四棱锥P-ABCD的底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=2BC=2CD=2,PA=PD,PA⊥PD,PB=PC.(Ⅰ)求证:平面PAD⊥平面ABCD;
(Ⅱ)求直线PB与平面PAD所成角的正切值.
分析:(Ⅰ)取AD中点M,BC中点N,连接MN、PN、PM,先证明BC⊥平面PMN,可得BC⊥PM,同理可得PM⊥AD,利用线面垂直的判定,可得PM⊥平面ABCD,根据面面垂直的判定,可得平面PAD⊥平面ABCD.
(Ⅱ)连接BD,证明BD⊥平面PAD,则∠BPD为直线PB与平面PAD所成角,从而可求直线PB与平面PAD所成角的正切值.
(Ⅱ)连接BD,证明BD⊥平面PAD,则∠BPD为直线PB与平面PAD所成角,从而可求直线PB与平面PAD所成角的正切值.
解答:(Ⅰ)证明:取AD中点M,BC中点N,连接MN、PN、PM,
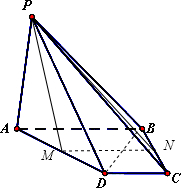
则MN是直角梯形ABCD的中位线,∴MN∥AB∥CD,
∵BC⊥AB,∴MN⊥BC,
∵PB=PC,∴△PBC是等腰△,∴PN⊥BC,
∵PN∩NB=N,∴BC⊥平面PMN,
∵PM?平面PMN,∴BC⊥PM,
同理PA=PD,∴PM⊥AD,
∵四边形ABCD是梯形,∴在平面ABCD上,AD和BC不平行必相交于一点F,
∴PM⊥平面ABCD,
∵PM?平面PAD,∴平面PAD⊥平面ABCD.
(Ⅱ)连接BD,则在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD=2,则BD⊥AD,BD=AD=
,
∵BD⊥AD,平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD
∴BD⊥平面PAD
∴∠BPD为直线PB与平面PAD所成角
∵PA=PD,PA⊥PD
∴PB=1
∴tan∠BPD=
=
.

则MN是直角梯形ABCD的中位线,∴MN∥AB∥CD,
∵BC⊥AB,∴MN⊥BC,
∵PB=PC,∴△PBC是等腰△,∴PN⊥BC,
∵PN∩NB=N,∴BC⊥平面PMN,
∵PM?平面PMN,∴BC⊥PM,
同理PA=PD,∴PM⊥AD,
∵四边形ABCD是梯形,∴在平面ABCD上,AD和BC不平行必相交于一点F,
∴PM⊥平面ABCD,
∵PM?平面PAD,∴平面PAD⊥平面ABCD.
(Ⅱ)连接BD,则在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD=2,则BD⊥AD,BD=AD=
| 2 |
∵BD⊥AD,平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD
∴BD⊥平面PAD
∴∠BPD为直线PB与平面PAD所成角
∵PA=PD,PA⊥PD
∴PB=1
∴tan∠BPD=
| BD |
| PD |
| 2 |
点评:本题考查线面垂直、面面垂直、考查线面角,掌握线面垂直、面面垂直的判定方法,正确作出线面角是关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
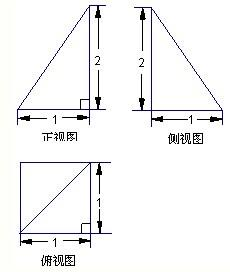 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
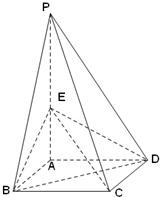 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: