题目内容
四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,∠BAD=120°,PA=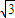 ,∠ACB=90°.
,∠ACB=90°.(Ⅰ)求证:BC⊥平面PAC;
(Ⅱ)求二面角D-PC-A的平面角的余弦值.
【答案】分析:(Ⅰ)由PA⊥底面ABCD,BC?底面ABCD,知PA⊥BC,由此能够证明BC⊥平面PAC.
(Ⅱ)法一:由∠BAD=120°,AB∥CD,知∠ADC=60°,由AD=CD=1,知△ADC为正三角形以A为原点,CD边的中线所在直线为x轴,直线AB为y轴,AP为z轴建立空间直角坐标系,利用向量法能够求出二面角D-PC-A的平面角的余弦值.
法二:(三垂线法作二面角的平面角)取AC中点M,则DM⊥AC,又PA⊥DM,所以DM⊥面PAC,从而DM⊥PC,作MN⊥PC于N,则PC⊥面DMN,所以∠DNM即为二面角D-PC-A的平面角,由此能求出二面角D-PC-A的平面角的余弦值.
解答:解:(Ⅰ)证明:∵PA⊥底面ABCD,BC?底面ABCD,
∴PA⊥BC,又AB∥CD,AD=CD=1,∠BAD=120°,∠ACB=90°,
所以BC⊥AC,而AC∩PA=A,
所以BC⊥平面PAC;
(Ⅱ)(方法一)∵∠BAD=120°,AB∥CD,
∴∠ADC=60°,又AD=CD=1,
∴△ADC为正三角形
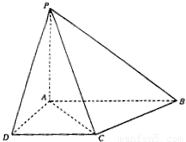
以A为原点,CD边的中线所在直线为x轴,直线AB为y轴,AP为z轴建立空间直角坐标系如图所示,
则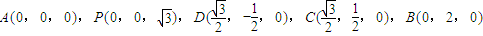 ,
,
由(1)取面PAC的法向量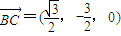 ,
,
由于AB∥CD,知AB∥面PCD,
故可设面PCD的法向量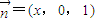 ,
,
则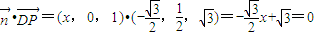 ,
,
∴x=2,即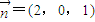 ,
,
∴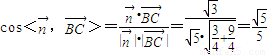 ,
,
所以,二面角D-PC-A的平面角的余弦值为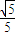 .
.
(方法二:三垂线法作二面角的平面角)取AC中点M,
则DM⊥AC,又PA⊥DM,
所以DM⊥面PAC,从而DM⊥PC,
作MN⊥PC于N,则PC⊥面DMN,
所以∠DNM即为二面角D-PC-A的平面角,
由题设条件求得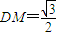 ,
,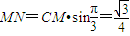 ,
,
所以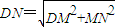 =
=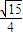 ,
,
于是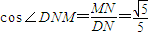 ,
,
即二面角D-PC-A的平面角的余弦值为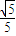 .
.
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,仔细解答,注意合理地选择解题方法.
(Ⅱ)法一:由∠BAD=120°,AB∥CD,知∠ADC=60°,由AD=CD=1,知△ADC为正三角形以A为原点,CD边的中线所在直线为x轴,直线AB为y轴,AP为z轴建立空间直角坐标系,利用向量法能够求出二面角D-PC-A的平面角的余弦值.
法二:(三垂线法作二面角的平面角)取AC中点M,则DM⊥AC,又PA⊥DM,所以DM⊥面PAC,从而DM⊥PC,作MN⊥PC于N,则PC⊥面DMN,所以∠DNM即为二面角D-PC-A的平面角,由此能求出二面角D-PC-A的平面角的余弦值.
解答:解:(Ⅰ)证明:∵PA⊥底面ABCD,BC?底面ABCD,
∴PA⊥BC,又AB∥CD,AD=CD=1,∠BAD=120°,∠ACB=90°,
所以BC⊥AC,而AC∩PA=A,
所以BC⊥平面PAC;
(Ⅱ)(方法一)∵∠BAD=120°,AB∥CD,
∴∠ADC=60°,又AD=CD=1,
∴△ADC为正三角形
以A为原点,CD边的中线所在直线为x轴,直线AB为y轴,AP为z轴建立空间直角坐标系如图所示,
则
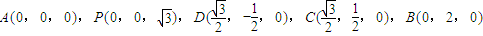 ,
,由(1)取面PAC的法向量
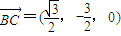 ,
,由于AB∥CD,知AB∥面PCD,
故可设面PCD的法向量
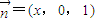 ,
,则
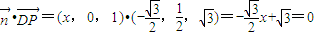 ,
,∴x=2,即
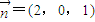 ,
,∴
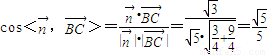 ,
,所以,二面角D-PC-A的平面角的余弦值为
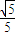 .
.(方法二:三垂线法作二面角的平面角)取AC中点M,
则DM⊥AC,又PA⊥DM,
所以DM⊥面PAC,从而DM⊥PC,
作MN⊥PC于N,则PC⊥面DMN,
所以∠DNM即为二面角D-PC-A的平面角,
由题设条件求得
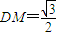 ,
,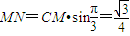 ,
,所以
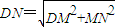 =
=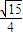 ,
,于是
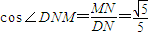 ,
,即二面角D-PC-A的平面角的余弦值为
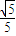 .
.点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,仔细解答,注意合理地选择解题方法.

练习册系列答案
相关题目
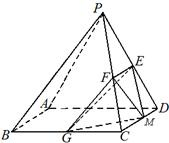 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.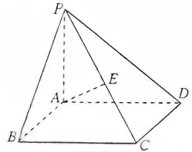 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2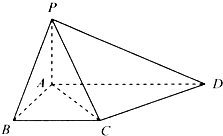 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.